【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 的中点,
的中点,![]() 且交
且交![]() 于点
于点![]() ,求证:
,求证:![]() 是
是![]() 的中位线.
的中位线.
参考答案:
【答案】证明见解析.
【解析】
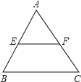
过点B作BG∥CF交FE的延长线于G,判断出四边形BCFG是平行四边形,根据平行四边形的对边相等可得BG=CF,根据两直线平行,内错角相等可得∠A=∠EBG,再利用“边角边”证明△AEF和△BEG全等,根据全等三角形对应边相等可得BG=AF,从而得到AF=CF,再根据三角形的中位线的定义证明.
如图,过点B作BG∥CF交FE的延长线于G.
∵EF∥BC,∴四边形BCFG是平行四边形,∴BG=CF,∴BG∥CF,∴∠A=∠EBG.
∵点E是AB的中点,∴AE=BE.
在△AEF和△BEG中,∵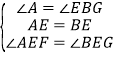 ,∴△AEF≌△BEG(ASA),∴BG=AF,∴AF=CF.
,∴△AEF≌△BEG(ASA),∴BG=AF,∴AF=CF.
又∵点E是AB的中点,∴EF是△ABC的中位线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
 如图①,在
如图①,在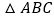 中,
中,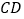 为角平分线,
为角平分线,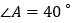 ,
,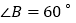 ,求证:
,求证: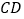 是
是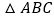 的完美分割线;
的完美分割线;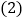 如图②,在
如图②,在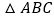 中,
中,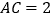 ,
,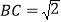 ,
,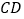 是
是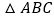 的完美分割线,且
的完美分割线,且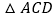 是以
是以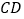 为底边的等腰三角形,求完美分割线
为底边的等腰三角形,求完美分割线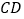 的长.
的长.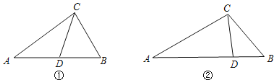
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,AB=AC=9,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为___________;

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)是一个长为2m,宽为2n的长方形,沿图中虚线剪成四个均匀的小长方形,然后按图(2)形状拼成一个正方形.
(1)你认为图(2)中的阴影部分的正方形的边长等于多少?
(2)观察图(2),你能写出下列三个代数式之间的等量关系吗?代数式:
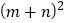 ,
,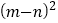 ,
,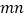 ;
;(3)已知:
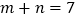 ,
,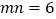 ,求
,求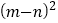 的值.
的值.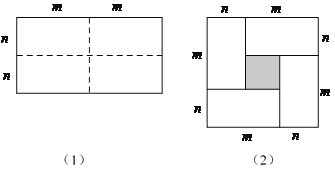
-
科目: 来源: 题型:
查看答案和解析>>【题目】(问题情境)如图
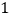 ,
,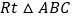 中,
中,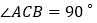 ,
,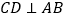 ,我们可以利用
,我们可以利用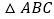 与
与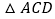 相似证明
相似证明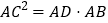 ,这个结论我们称之为射影定理,试证明这个定理;
,这个结论我们称之为射影定理,试证明这个定理;(结论运用)如图
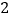 ,正方形
,正方形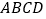 的边长为
的边长为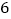 ,点
,点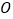 是对角线
是对角线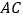 、
、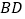 的交点,点
的交点,点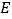 在
在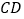 上,过点
上,过点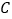 作
作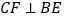 ,垂足为
,垂足为 ,连接
,连接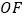 ,
, (1)试利用射影定理证明
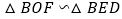 ;
;(2)若
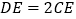 ,求
,求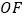 的长.
的长.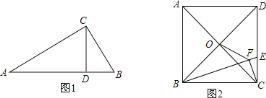
-
科目: 来源: 题型:
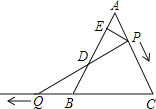
查看答案和解析>>【题目】如图,
 是边长为6的等边三角形,
是边长为6的等边三角形,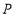 是
是 边上一动点,由
边上一动点,由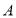 向
向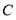 运动(与
运动(与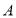 、
、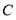 不重合),
不重合),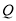 是
是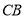 延长线上一动点,与点
延长线上一动点,与点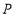 同时以相同的速度由
同时以相同的速度由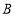 向
向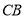 延长线方向运动(
延长线方向运动(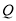 不与
不与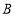 重合),过
重合),过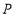 作
作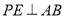 于
于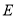 ,连接
,连接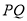 交
交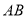 于
于 .
.
(1)当
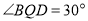 时,求
时,求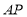 的长;
的长;(2)在运动过程中线段
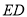 的长是否发生变化?如果不变,求出线段
的长是否发生变化?如果不变,求出线段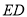 的长;如果发生改变,请说明理由.
的长;如果发生改变,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工程,乙工程队单独先做10天后,再由甲、乙两个工程队合作20天就能完成全部工作,已知甲工程队单独完成此工程所需天数是乙工程队单独完成此工程所需天数的
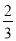 .
.(1)求甲、乙工程队单独完成此工程各需多少天;
(2)甲工程队每天的费用为0.67万元,乙工程每天的费用为0.33万元,该工程的预算费用为20万元,若甲、乙工程队一起合作完成该工程,请问工程费用是否够用?若不够用,应追加多少万元?
相关试题

