【题目】如图1,在平面直角坐标系中,抛物线经过坐标原点O,点A(6,﹣6 ![]() ),且以y轴为对称轴.
),且以y轴为对称轴.
(1)求抛物线的解析式;
(2)如图2,过点B(0,﹣ ![]() )作x轴的平行线l,点C在直线l上,点D在y轴左侧的抛物线上,连接DB,以点D为圆心,以DB为半径画圆,⊙D与x轴相交于点M,N(点M在点N的左侧),连接CN,当MN=CN时,求锐角∠MNC的度数;
)作x轴的平行线l,点C在直线l上,点D在y轴左侧的抛物线上,连接DB,以点D为圆心,以DB为半径画圆,⊙D与x轴相交于点M,N(点M在点N的左侧),连接CN,当MN=CN时,求锐角∠MNC的度数;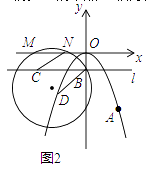
(3)如图3,在(2)的条件下,平移直线CN经过点A,与抛物线相交于另一点E,过点A作x轴的平行线m,过点(﹣3,0)作y轴的平行线n,直线m与直线n相交于点S,点R在直线n上,点P在EA的延长线上,连接SP,以SP为边向上作等边△SPQ,连接RQ,PR,若∠QRS=60°,线段PR的中点K恰好落在抛物线上,求Q点坐标.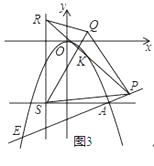
参考答案:
【答案】
(1)
解:设过坐标原点O,点A(6,﹣6 ![]() ),且以y轴为对称轴的抛物线为y=ax2,
),且以y轴为对称轴的抛物线为y=ax2,
则﹣6 ![]() =36a,
=36a,
∴a=﹣ ![]() ,
,
∴y=﹣ ![]() x2
x2
(2)
解:如图2中,作CF⊥MN于F,设⊙D与x轴的交点为(x,0),D(m,﹣ ![]() m2).
m2).
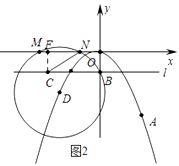
则有(x﹣m)2+( ![]() m2)2=m2+(﹣
m2)2=m2+(﹣ ![]() m2+
m2+ ![]() )2,
)2,
整理得x2﹣2mx+m2﹣3=0,
∴x=m+ ![]() 或m﹣
或m﹣ ![]() ,
,
∴N(m+ ![]() ,0),M(m﹣
,0),M(m﹣ ![]() ,0)
,0)
∴MN=2 ![]() ,
,
在Rt△CFN中,∵∠CFN=90°,CN=MN=2 ![]() ,CF=
,CF= ![]() ,
,
∴CN=2CF,
∴∠CNF=30°
(3)
解:如图3中,

由题意可知平移直线CN经过点A的直线的解析式为y= ![]() x﹣8
x﹣8 ![]() ,
,
记直线y= ![]() x﹣8
x﹣8 ![]() 与直线x=﹣3的交点为G,则G(﹣3,﹣9
与直线x=﹣3的交点为G,则G(﹣3,﹣9 ![]() ),
),
∵m∥x轴,且过点A(6,﹣6 ![]() ),
),
∴S(﹣3,﹣6 ![]() ),
),
∴SG=3 ![]() ,AS=9,
,AS=9,
∴tan∠2= ![]() =
= ![]() ,
,
∴∠2=60°,
∴∠1=30°,
∵∠QRS=60°
∴∠QRS=∠2,
∵∠RSQ+∠QSP=∠2+∠SPG,∠QSP=∠2=60°,
∴∠3=∠4,
在△SQR和△PSG中,
 ,
,
∴△SQR≌△PSH
∴SR=PG,RQ=SG,
∴RQ=SG=3 ![]() ,作DQ⊥n于D,
,作DQ⊥n于D,
∴QRD=60°,
∴DQ= ![]() DR=
DR= ![]() RQ=
RQ= ![]() ,
,
∴RD= ![]() QR=
QR= ![]() ,
,
∵n是过(﹣3,0)与y轴平行的直线,设R(﹣3,b),记n与x轴的交点为M,则RM=b,
∵S(﹣3,﹣6 ![]() ),
),
∴MS=6 ![]() ,
,
∴SR=RM+MS=b+6 ![]() =PG,作PH⊥n于H,
=PG,作PH⊥n于H,
∵∠2=60°,
∴GH= ![]() PG=
PG= ![]() (b+6
(b+6 ![]() ),
),
∴MH=MG﹣HG=9 ![]() ﹣
﹣ ![]() (b+6
(b+6 ![]() )=6
)=6 ![]() ﹣
﹣ ![]() b,
b,
∴P(6+ ![]() b,
b, ![]() b﹣6
b﹣6 ![]() ),
),
∵K是PR中点,
∴K( ![]() +
+ ![]() b,
b, ![]() b﹣3
b﹣3 ![]() ),
),
为了方便,记K(x,y),即x= ![]() +
+ ![]() b,y=
b,y= ![]() b﹣3
b﹣3 ![]() ,消去b得y=
,消去b得y= ![]() x﹣
x﹣ ![]()
![]() ,
,
∴中点K在直线y= ![]() ﹣
﹣ ![]() 上运动,
上运动,
由 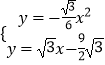 消去y得到x2+6x﹣27=0,
消去y得到x2+6x﹣27=0,
∴x=3或﹣9(舍弃),
∴x=3,代入x= ![]() +
+ ![]() b得到b=2
b得到b=2 ![]() ,
,
∴RM=2 ![]() ,DM=RM﹣RD=2
,DM=RM﹣RD=2 ![]() ﹣
﹣ ![]()
![]() =
= ![]()
![]() ,
,
∵ ![]() ﹣3=
﹣3= ![]() ,
,
∴点Q的坐标为( ![]() ,
, ![]()
![]() )
)
【解析】(1)设过坐标原点O,点A(6,﹣6 ![]() ),且以y轴为对称轴的抛物线为y=ax2 , 点A代入求出a即可.(2)如图2中,作CF⊥MN于F,设⊙D与x轴的交点为(x,0),D(m,﹣
),且以y轴为对称轴的抛物线为y=ax2 , 点A代入求出a即可.(2)如图2中,作CF⊥MN于F,设⊙D与x轴的交点为(x,0),D(m,﹣ ![]() m2),根据半径相等列出方程,求出M、N坐标,推出MN=2
m2),根据半径相等列出方程,求出M、N坐标,推出MN=2 ![]() ,在Rt△CFN中,由CN=2CF推出∠FNC=30°即可解决问题.(3)如图3中,由题意可知平移直线CN经过点A的直线的解析式为y=
,在Rt△CFN中,由CN=2CF推出∠FNC=30°即可解决问题.(3)如图3中,由题意可知平移直线CN经过点A的直线的解析式为y= ![]() x﹣8
x﹣8 ![]() ,记直线y=
,记直线y= ![]() x﹣8
x﹣8 ![]() 与直线x=﹣3的交点为G,则G(﹣3,﹣9
与直线x=﹣3的交点为G,则G(﹣3,﹣9 ![]() ),由△SQR≌△PSH,推出SR=PG,RQ=SG,推出RQ=SG=3
),由△SQR≌△PSH,推出SR=PG,RQ=SG,推出RQ=SG=3 ![]() ,作DQ⊥n于D,记n与x轴的交点为M,则RM=b,由S(﹣3,﹣6
,作DQ⊥n于D,记n与x轴的交点为M,则RM=b,由S(﹣3,﹣6 ![]() ),推出MS=6
),推出MS=6 ![]() ,可得P(6+
,可得P(6+ ![]() b,
b, ![]() b﹣6
b﹣6 ![]() ),再求出PR中点k坐标,证明k在直线y=
),再求出PR中点k坐标,证明k在直线y= ![]() ﹣
﹣ ![]() 上运动,由
上运动,由 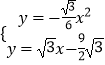 消去y得到x2+6x﹣27=0,x=3或﹣9(舍弃),x=3,代入x=
消去y得到x2+6x﹣27=0,x=3或﹣9(舍弃),x=3,代入x= ![]() +
+ ![]() b得到b=2
b得到b=2 ![]() ,由此即可解决问题.
,由此即可解决问题.
【考点精析】关于本题考查的二次函数的图象和二次函数的性质,需要了解二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】⊙O是△ABC的外接圆,AB是直径,过
 的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
(1)如图1,求证:AG=CP;
(2)如图2,过点P作AB的垂线,垂足为点H,连接DH,求证:DH∥AG;
(3)如图3,连接PA,延长HD分别与PA、PC相交于点K、F,已知FK=2,△ODH的面积为2 ,求AC的长.
,求AC的长. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=4cm,AC=BD=3cm.∠CAB=∠DBA=60°,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s),则点Q的运动速度为 cm/s,使得A、C、P三点构成的三角形与B、P、Q三点构成的三角形全等.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个三角形的两条边长分别是1cm和2cm,一个内角为40度.
(1)请你借助图1画出一个满足题设条件的三角形;
(2)你是否还能画出既满足题设条件,又与(1)中所画的三角形不全等的三角形?若能,请你在图1的右边用“尺规作图”作出所有这样的三角形;若不能,请说明理由;
(3)如果将题设条件改为“三角形的两条边长分别是3cm和4cm,一个内角为40°”,那么满足这一条件,且彼此不全等的三角形共有几个.
友情提醒:请在你画的图中标出已知角的度数和已知边的长度,“尺规作图”不要求写作法,但要保留作图痕迹.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,△AOB为顶点A,B的坐标分别为A(0,4),B(﹣3,0),按要求解答下列问题.

(1)①在图中,先将△AOB向上平移6个单位,再向右平移3个单位,画出平移后的△A1O1B1;(其中点A,O,B的对应点为A1 , O1 , B1)
②在图中,将△A1O1B1绕点O1顺时针旋转90°,画出旋转后的Rt△A2O1B2;(其中点A1 , B1的对应点为A2 , B2)
(2)直接写出点A2 , B2的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】在新晚报举办的“万人户外徒步活动”中,为统计参加活动人员的年龄情况,从参加人员中随机抽取了若干人的年龄作为样本,进行数据统计,制成如图的条形统计图和扇形统计图(部分).
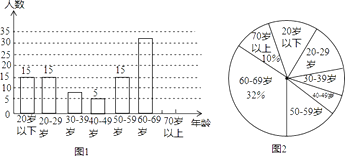
(1)本次活动统计的样本容量是多少?
(2)求本次活动中70岁以上的人数,并补全条形统计图;
(3)本次参加活动的总人数约为12000人,请你估算参加活动人数最多的年龄段的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,△ABC是直角三角形,∠ACB=90°,点B、C都在第一象限内,CA⊥x轴,垂足为点A,反比例函数y1=
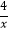 的图象经过点B;反比例函数y2=
的图象经过点B;反比例函数y2= 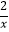 的图象经过点C(
的图象经过点C( 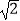 ,m).
,m).
(1)求点B的坐标;
(2)△ABC的内切圆⊙M与BC,CA,AB分别相切于D,E,F,求圆心M的坐标.
相关试题

