【题目】如图,已知正方形![]() ,对角线
,对角线![]() 的中点为
的中点为![]() ,点
,点![]() 同时是正方形
同时是正方形![]() 的一个顶点,
的一个顶点,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,若这两个正方形的边长都是3,将正方形
,若这两个正方形的边长都是3,将正方形![]() 绕点
绕点![]() 转动.
转动.

(1)两个正方形重叠部分的面积________改变(填“会”或“不会”)
(2)两个正方形重叠部分的面积若改变,说明理由;若不改变,直接写出重叠部分的面积.请将答案写在横线上________________.
参考答案:
【答案】不会 ![]()
【解析】
(1)由“ASA”可证△AOE≌△BOF,可得S△AOE=S△BOF,即可求解;
(2)求出正方形的面积,即可求解.
解:(1)连接BO,
在正方形ABCD中,AO=BO,∠AOB=90°,∠OAB=∠OBC=45°,
∵∠AOE+∠EOB=90°,∠BOF+∠EOB=90°,
∴∠AOE=∠BOF,且OA=OB,∠OAE=∠OBF=45°
∴△AOE≌△BOF(ASA).
∴S△AOE=S△BOF,
∴S四边形OEBF=S△EOB+S△OBF=S△EOB+S△AOE=S△AOB=![]() S正方形ABCD,
S正方形ABCD,
故答案为:不会;
(2)∵两个正方形的边长都是3,
∴重叠部分的面积=![]() ×9=
×9=![]() .
.
故答案为:(1)不会;(2)![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果顺次连接一个四边形各边的中点,得到的新四边形是矩形,则原四边形一定是( )
A.平行四边形B.矩形
C.对角线互相垂直的四边形D.对角线相等的四边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当方法解下列方程:
(1)(3x+1)2﹣9=0
(2)x2+4x﹣1=0
(3)3x2﹣2=4x
(4)(y+2)2=1+2y.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了尽快的适应中招体考项目,现某校初二(1)班班委会准备筹集1800元购买A、B两种类型跳绳供班级集体使用.
(1)班委会决定,购买A种跳绳的资金不少于B种跳绳资金的2倍,问最多用多少资金购买B种跳绳?
(2)经初步统计,初二(1)班有25人自愿参与购买,那么平均每生需交72元.初三(1)班了解情况后,把体考后闲置的跳绳赠送了若干给初二(1)班,这样只需班级共筹集1350元.经初二(1)班班委会进一步宣传,自愿参与购买的学生在25人的基础上增加了4a%.则每生平均交费在72元基础上减少了2.5a%,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋中装有5个黄球、13个黑球和22个红球,这些球除颜色外其他都相同.
(1)求从袋中摸出一个球是黄球的概率;
(2)求从袋中摸出一个球不是红球的概率;
(3)现在从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后,若从袋中摸出一个球是黄球的概率为
 ,则取出了多少个黑球?
,则取出了多少个黑球? -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校八年级学生参加体育锻炼的情况,随机调查了该校部分学生每周参加体育锻炼的时间,并进行了统计,绘制成图1和图2两幅尚不完整的统计图.

(1)本次共调查学生 人;
(2)这组数据的众数是 ;
(3)请你将图2的统计图补充完整;
(4)若该校八年级共有650人,请根据样本数据,估计每周参加体育锻炼时间为6小时的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校举行数学竞赛,需购买
 两种奖品共160件,其中
两种奖品共160件,其中 种奖品的单价为12元,
种奖品的单价为12元, 种奖品的单价为8元,且购买
种奖品的单价为8元,且购买 种奖品的数量不大于
种奖品的数量不大于 种奖品数量的3倍,假设购买
种奖品数量的3倍,假设购买 种奖品的数量为
种奖品的数量为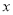 件.
件.(1)根据题意填空:
购买
 种奖品的费用为___(元);
种奖品的费用为___(元);购买
 种奖品的费用为___(元);
种奖品的费用为___(元);(2)若购买两种奖品所需的总费用为
 元,试求
元,试求 与
与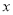 的函数关系式,并求出
的函数关系式,并求出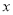 的取值范围;
的取值范围;(3)问
 两种奖品各购买多少件时所需的总费用最少,并求出最少费用.
两种奖品各购买多少件时所需的总费用最少,并求出最少费用.
相关试题

