【题目】在![]() 中,
中,![]() ,
,![]() 的垂直平分线与
的垂直平分线与![]() 所在的直线相交所得到的锐角为
所在的直线相交所得到的锐角为![]() ,则
,则![]() 等于______________度.
等于______________度.
参考答案:
【答案】65°或25°
【解析】
(1)当△ABC是锐角三角形时,根据题目条件得到∠A=50°,利用△ABC是等腰三角形即可求解;(2)当△ABC是钝角三角形时,同理可得即可得出结果.
解:(1)当△ABC是锐角等腰三角形时,如图1所示
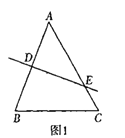
由题知:DE⊥AB,AD=DB,∠AED=40°
∴∠A=180°-90°-40°=50°
∵AB=AC
∴△ABC是等腰三角形
∴∠ABC=∠ACB
∴∠ABC=(180°-50°)÷2=65°
(2)当△ABC是钝角三角形时,如图2所示
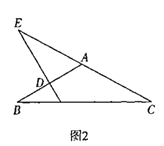
由题知:DE⊥AB,AD=DB,∠AED=40°
∴∠AED+∠ADE=∠BAC
∴∠BAC=90°+40°=130°
∵AB=AC
∴△ABC是等腰三角形
∴∠ABC=∠ACB
∴∠ABC=(180°-130°)÷2=25°
∴∠ABC=65°或25°
故答案为:65°或25°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2﹣x+a(a>0),当自变量x取m时,其相应的函数值小于0,那么下列结论中正确的是( )
A.m﹣1>0
B.m﹣1<0
C.m﹣1=0
D.m﹣1与0的大小关系不确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠BAC=108°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( )

A.20°B.24°C.30°D.36°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有下列四个条件:①AB=BC,②∠ABC=90
 ,③AC=BD,④AC⊥BD.从中选取两个作为补充条件,使□BCD为正方形(如图).现有下列四种选法,其中错误的是 ( )
,③AC=BD,④AC⊥BD.从中选取两个作为补充条件,使□BCD为正方形(如图).现有下列四种选法,其中错误的是 ( )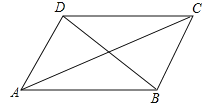
A. ②③ B. ②④ C. ①② D. ①③
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B两地相距4千米.上午8:00,甲从A地出发步行到B地,8:20乙从B地出发骑自行车到A地,甲、乙两人离A地的距离(千米)与甲所用的时间(分)之间的关系如图所示.由图中的信息可知,乙到达A地的时间为____.

相关试题

