【题目】已知关于x的一元二次方程x2+2x+2k﹣4=0有两个不相等的实数根.
(1)求k的取值范围:
(2)若k为正整数,且该方程的根都是整数,求k的值及该方程的根.
参考答案:
【答案】
(1)
解:依题意得△=22﹣4(2k﹣4)>0,
解得:k< ![]()
(2)
解:因为k< ![]() 且k为正整数,
且k为正整数,
所以k=1或2,
当k=1时,方程化为x2+2x﹣4=0,△=18,此方程无整数根;
当k=2时,方程化为x2+2x=0 解得x1=0,x2=﹣2,
所以k=2,方程的有整数根为x1=0,x2=﹣2
【解析】(1)根据判别式的意义得到△=22﹣4(2k﹣4)>0,然后解不等式即可得到k的范围;(2)先确定整数k的值为1或2,然后把k=1或k=2代入方程得到两个一元二次方程,然后解方程确定方程有整数解的方程即可.
【考点精析】根据题目的已知条件,利用求根公式的相关知识可以得到问题的答案,需要掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400 m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用是0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:(1)
 ;(2)
;(2) ;(3)
;(3) +1=
+1=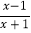 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程(m﹣1)x2+x+1=0有实数根,则m的取值范围是( )
A.m
B.m>1
C.m<1
D.m 且m≠1
且m≠1 -
科目: 来源: 题型:
查看答案和解析>>【题目】在“文博会”期间,某公司展销如图所示的长方形工艺品,该工艺品长60cm,宽40cm,中间镶有宽度相同的三条丝绸花边.

(1)若丝绸花边的面积为650cm2 , 求丝绸花边的宽度;
(2)已知该工艺品的成本是40元/件,如果以单价100元/件销售,那么每天可售出200件,另每天所需支付的各种费用2000元,根据销售经验,如果将销售单价降低1元,每天可多售出20件,同时,为了完成销售任务,该公司每天至少要销售800件,那么该公司应该把销售单价定为多少元,才能使每天所获销售利润最大?最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】为了迎接运动会,某校八年级学生开展了“短跑比赛”。甲、乙两人同时从A地出发,沿同一条道路去B地,途中都使用两种不同的速度
 与
与 。
。甲前一半的路程使用速度
 ,另一半的路程使用速度
,另一半的路程使用速度 ;乙前一半的时间用速度
;乙前一半的时间用速度 ,另一半的时间用速度
,另一半的时间用速度 。
。(1)甲、乙二人从A地到达B地的平均速度分别为
 ;则
;则 ___________,
___________, ____________
____________(2)通过计算说明甲、乙谁先到达B地?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
相关试题

