【题目】在平面直角坐标系中,点B、A分别在x轴和y轴上,连接AB,已知∠ABO=60°,BC平分∠ABO交y轴于点C,且BC=8.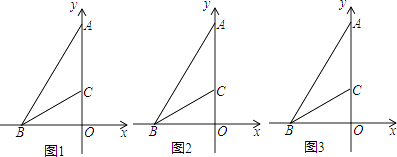
(1)求点A的坐标;
(2)点P从点B出发,沿射线BC方向以每秒2个长度单位的速度运动,过点P作PQ⊥y轴于Q,设点P的运动时间为t秒,试用t表示线段CQ的长;
(3)点D是点B关于y轴的对称点,在(2)的条件下,连接OP、DQ、CD,当 ![]() 时,求t的值.
时,求t的值.
参考答案:
【答案】
(1)
解:∵∠ABO=60°,BC是角平分线,
∴∠ABC=∠CBO=30°,
在直角△BOC中,OC=BCsin∠CBO= ![]() BC=4,即C的坐标是(0,4).
BC=4,即C的坐标是(0,4).
又∵直角△ABO中,∠BAO=90°﹣∠ABO=90°﹣60°=30°,
∴∠BAO=∠ABC=30°,
∴AC=BC=8,
∴OA=8+4=12,
∴A的坐标是(0,12)
(2)
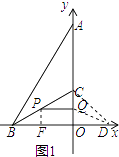
解:当0≤t≤4时,如图1,P在BC上,BP=2t,则PC=8﹣2t,
在直角△PCQ中,∠CPQ=∠CBO=30°,
则CQ= ![]() PC=
PC= ![]() (8﹣2t)=4﹣t;
(8﹣2t)=4﹣t;
当t>4时,P在BC的延长线上,如图2.
BP=2t,则CP=2t﹣8,
在直角△PCQ中,∠CPQ=30°,CQ= ![]() PC=
PC= ![]() (2t﹣8)=4﹣4
(2t﹣8)=4﹣4
(3)
解:在直角△BOC中,OB=BCcos∠CBO=8× ![]() =4
=4 ![]() ,则B的坐标是(﹣4
,则B的坐标是(﹣4 ![]() ,0),则D的坐标是(4
,0),则D的坐标是(4 ![]() ,0).
,0).
当0≤t≤4时,如图1,P在线段BC上,作PF⊥OB于点F.则PF= ![]() BP=t,则S△BOP=
BP=t,则S△BOP= ![]() ×4
×4 ![]() t=2
t=2 ![]() t,
t,
CQ=4﹣t,则S△DCQ= ![]() (4﹣t)×4
(4﹣t)×4 ![]() =﹣2
=﹣2 ![]() t+8
t+8 ![]() ,
,
当 ![]() 时,2
时,2 ![]() t=
t= ![]() (﹣2
(﹣2 ![]() t+8
t+8 ![]() ),解得:t=
),解得:t= ![]() ;
;
当t>4时P在BC的延长线上,如图2.作PF⊥OB于点F.则PF= ![]() BP=t,则S△BOP=
BP=t,则S△BOP= ![]() ×4
×4 ![]() t=2
t=2 ![]() t,
t,
CQ=4﹣t,则S△DCQ= ![]() (t﹣4)×4
(t﹣4)×4 ![]() =2
=2 ![]() t﹣8
t﹣8 ![]() ,
,
当 ![]() 时,2
时,2 ![]() t=
t= ![]() (2
(2 ![]() t﹣8
t﹣8 ![]() ),解得:t=9.
),解得:t=9.
总之,t= ![]() 或9.
或9.
【解析】(1)首先在直角△BOC中,利用三角函数求得OC的长,然后证明BC=AC,则求得OA的长,得到A的坐标;(2)分成P在线段BC上和在BC的延长线上两种情况进行讨论,利用三角函数求解;(3)同(2)分成两种情况讨论,根据三角形面积公式利用t表示出△BPO和△DCQ的面积,然后解方程即可求解.
【考点精析】掌握锐角三角函数的定义是解答本题的根本,需要知道锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABD是等腰三角形,AB=AD,将△ABD沿BD翻折得△CBD,点P是线段BD上一点,
(1)如图1,连接PA、PC,求证:CP=AP;
(2)如图2,连接PA,若∠BAP=90°时,作∠DPF=45°,线段PF交线段CD于F,求证:AD=AP+DF;
(3)如图3,∠ABD=30°,连接AP并延长交CD于M,若∠BAM=90°,在BD上取一点Q,且DQ=3BQ,连BM、CQ,当BM= 时,求CQ的长.
时,求CQ的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的不等式(a-2)x>a-2的解集是x>1,则a的取值范围是( )
A. a>1 B. a<1 C. a>2 D. a<2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣
 x2+bx+c的图象与x轴的正半轴相交于点A(2,0)和点B、与y轴相交于点C,它的顶点为M、对称轴与x轴相交于点N.
x2+bx+c的图象与x轴的正半轴相交于点A(2,0)和点B、与y轴相交于点C,它的顶点为M、对称轴与x轴相交于点N.(1)用b的代数式表示顶点M的坐标;
(2)当tan∠MAN=2时,求此二次函数的解析式及∠ACB的正切值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合).以AD为边作正方形ADEF,连接CF.
(1)如图1,当点D在线段BC上时,求证:BD⊥CF.BD=CF.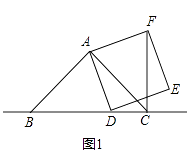
(2)如图2,当点D在线段BC的延长线上时,其它条件不变,第(1)问结论还成立吗?并说明理由.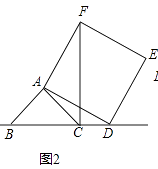
(3)如图3,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC的两侧,其它条件不变: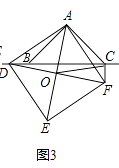
①请直接写出CF、BC、CD三条线段之间的关系.
②若连接正方形对角线AE、DF,交点为O,连接OC,探究△AOC的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】将点A(-1,2)沿x轴向右平移3个单位长度,再沿y轴向下平移4个单位长度后得到点A′的坐标为( )
A.(-4,-2 )
B.(2,-2 )
C.(-4,6 )
D.(2,6 ) -
科目: 来源: 题型:
查看答案和解析>>【题目】写出一个解集为x<-1,且未知数的系数为2的一元一次不等式:__________.
相关试题

