【题目】如图,△ABD是等腰三角形,AB=AD,将△ABD沿BD翻折得△CBD,点P是线段BD上一点,
(1)如图1,连接PA、PC,求证:CP=AP;
(2)如图2,连接PA,若∠BAP=90°时,作∠DPF=45°,线段PF交线段CD于F,求证:AD=AP+DF;
(3)如图3,∠ABD=30°,连接AP并延长交CD于M,若∠BAM=90°,在BD上取一点Q,且DQ=3BQ,连BM、CQ,当BM= ![]() 时,求CQ的长.
时,求CQ的长.
参考答案:
【答案】
(1)
证明:由翻折有,AD=CD,∠ADP=∠CDP,
在△ADP和△CDP中,
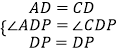
∴△ADP≌△CDP,
∴CP=AP
(2)
证明:连接PC,由(1)有,AP=CP,
由翻折有∠BCP=∠BAP=90°,
∴∠CBP+∠BPC=90°,
∵AD=AB=CB=CD,
∴∠CBP=∠CDP,
∴∠CDP+∠BPC=90°,
∵∠DPF=45°,
∴∠BPC+∠CPF=135°,
∴∠CPF=∠CDP+45°,
∵∠CFP=∠CDP+∠BPF=∠CDP+45°,
∴∠CPF=∠CFP,
∴CP=CF,
∴AD=CB=CF+FD=CP+FD=AP+FD
(3)
证明:如图,连接AQ,AC,
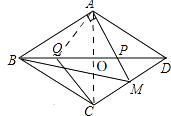
由(1)有,AQ=CQ,AP=CP,由翻折有AB=BC,AD=CD,
∵AB=AD,
∴AB=BC=CD=AD,
∴四边形ABCD是菱形,
∴AC⊥BD,OB=OD,OA=OC,∠BAD=120°,
∵DQ=3BQ,
∴BQ=OQ,
∴四边形CPAQ也是菱形,
∵∠BAM=90°,∠BAD=120°,
∴∠BAQ=∠DAM=30°,
∴∠ABD=∠CBD=∠ADB=∠CDB=30°,
∵∠ADM=60°,
∴∠AMD=90°,
∵△ACD等边三角形,
∴CD=2DM.
设DM=x,
∴CD=AD=AB=2DM=2x,AM= ![]() x,
x,
在Rt△ABM中,BM= ![]() ,
,
∴AB2+AM2=BM2,
∴(2x)2+( ![]() x)2=(
x)2=( ![]() )2,
)2,
∴x= ![]() 或x=﹣
或x=﹣ ![]() (舍),
(舍),
在RT△AOB中,∠ABD=30°,
∴OA= ![]() AB=x,OB=
AB=x,OB= ![]() x,
x,
∵OQ=BQ= ![]() OB=
OB= ![]() x,
x,
在RT△AOQ中,AQ= ![]() =
= ![]() x=
x= ![]() ,
,
∴CQ=AQ= ![]() .
.
【解析】(1)由翻折得到条件,直接判断出△ADP≌△CDP,即可;(2)由(1)结论CP=AP,用三角形的外角等于与它不相邻的两内角的和及平角的定义判断出∠CPF=∠CFP,得到CP=CF,即可;(3)由(1)的结论判断出四边形ABCD是菱形,继而判断出四边形AQCP也是菱形,利用勾股定理求出MN即可.
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识,掌握等腰三角形的两个底角相等(简称:等边对等角),以及对等腰三角形的判定的理解,了解如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2015年初,一列CRH5型高速车组进行了“300000公里正线运营考核”标志着中国高速快车从“中国制造”到“中国创造”的飞跃,将300000用科学记数法表示为( )
A.3×106
B.3×105
C.0.3×106
D.30×104 -
科目: 来源: 题型:
查看答案和解析>>【题目】哈市某花卉种植基地欲购进甲、乙两种君子兰进行培育,若购进甲种2株,乙种3株,则共需要成本1700元;若购进甲种3株,乙种1株,则共需要成本1500元.
(1)求甲乙两种君子兰每株成本分别为多少元?
(2)该种植基地决定在成本不超过30000元的前提下购进甲、乙两种君子兰,若购进乙种君子兰的株数比甲种君子兰的3倍还多10株,求最多购进甲种君子兰多少株? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在五边形ABCDE中,∠A+∠B+∠E=α,DP、CP分别平分∠EDC、∠BCD,则∠P的度数是( )

A. α﹣90°
α﹣90°
B.90°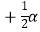
C.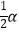
D.540°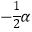
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的不等式(a-2)x>a-2的解集是x>1,则a的取值范围是( )
A. a>1 B. a<1 C. a>2 D. a<2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣
 x2+bx+c的图象与x轴的正半轴相交于点A(2,0)和点B、与y轴相交于点C,它的顶点为M、对称轴与x轴相交于点N.
x2+bx+c的图象与x轴的正半轴相交于点A(2,0)和点B、与y轴相交于点C,它的顶点为M、对称轴与x轴相交于点N.(1)用b的代数式表示顶点M的坐标;
(2)当tan∠MAN=2时,求此二次函数的解析式及∠ACB的正切值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点B、A分别在x轴和y轴上,连接AB,已知∠ABO=60°,BC平分∠ABO交y轴于点C,且BC=8.
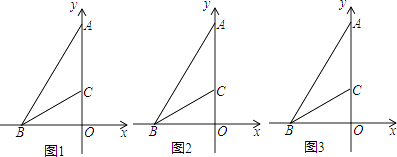
(1)求点A的坐标;
(2)点P从点B出发,沿射线BC方向以每秒2个长度单位的速度运动,过点P作PQ⊥y轴于Q,设点P的运动时间为t秒,试用t表示线段CQ的长;
(3)点D是点B关于y轴的对称点,在(2)的条件下,连接OP、DQ、CD,当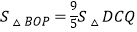 时,求t的值.
时,求t的值.
相关试题

