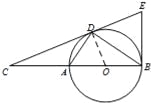
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6, ![]() .求BE的长.
.求BE的长.

参考答案:
【答案】(1)证明过程见解析;(2)2.5
【解析】试题分析:(1)连OD,OE,根据圆周角定理得到∠ADO+∠1=90°,而∠CDA=∠CBD,∠CBD=∠1,于是∠CDA+∠ADO=90°;(2)根据已知条件得到△CDA∽△CBD由相似三角形的性质得到![]() ,求得CD=4,由切线的性质得到BE=DE,BE⊥BC根据勾股定理列方程即可得到结论.
,求得CD=4,由切线的性质得到BE=DE,BE⊥BC根据勾股定理列方程即可得到结论.
试题解析:(1)连结OD, ∵OB=OD, ∴∠OBD=∠BDO, ∵∠CDA=∠CBD, ∴∠CDA=∠ODB,
又∵AB是⊙O的直径, ∴∠ADB=90°, ∴∠ADO+∠ODB=90°, ∴∠ADO+∠CDA=90°, 即∠CDO=90°,
∴OD⊥CD, ∵OD是⊙O半径, ∴CD是⊙O的切线
(2)∵∠C=∠C,∠CDA=∠CBD ∴△CDA∽△CBD ∴![]() ∵
∵![]() ,BC=6, ∴CD=4,
,BC=6, ∴CD=4,
∵CE,BE是⊙O的切线 ∴BE=DE,BE⊥BC ∴BE2+BC2=EC2,即BE2+62=(4+BE)2 解得:BE=2.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】某养殖户的养殖成本逐年增长,已知第一年的养殖成本为12万元,第3年的养殖成本为17万元.设每年平均增长的百分率为x,则下面所列方程中正确的是( )
A.12(1﹣x)2=17
B.17(1﹣x)2=12
C.17(1+x)2=12
D.12(1+x)2=17 -
科目: 来源: 题型:
查看答案和解析>>【题目】放风筝是大家喜爱的一种运动,星期天的上午小明在市政府广场上放风筝.如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝线AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为45°.已知点A,B,C在同一条水平直线上,请你求出小明此时所收回的风筝线的长度是多少米?(风筝线AD,BD均为线段,
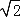 ≈1.414,
≈1.414,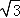 ≈1.732,最后结果精确到1米).
≈1.732,最后结果精确到1米).
-
科目: 来源: 题型:
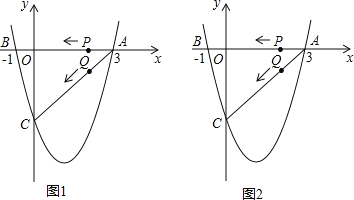
查看答案和解析>>【题目】如图1(注:与图2完全相同),二次函数y=
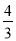 x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.(1)求该二次函数的解析式;
(2)设该抛物线的顶点为D,求△ACD的面积;
(3)若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动,当P,Q运动到t秒时,△APQ沿PQ所在的直线翻折,点A恰好落在抛物线上E点处,请直接判定此时四边形APEQ的形状,并求出E点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)先化简,再求值:(x﹣2)(3x2﹣1)﹣12x( x2﹣
x2﹣  x﹣3),其中x=﹣
x﹣3),其中x=﹣ 
(2)已知x2﹣5x=3,求2(x﹣1)(2x﹣1)﹣2(x+1)2+1的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解方程x2﹣2x﹣2=0,原方程应变形为( )
A. (x+1)2=3B. (x﹣1)2=3C. (x+1)2=1D. (x﹣1)2=1
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣1)2016+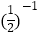 ﹣(π﹣3.14)0
﹣(π﹣3.14)0
(2)2a2b(﹣3b2c)÷(4ab3)
相关试题

