【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF= ![]() BC,连接CD和EF.
BC,连接CD和EF. 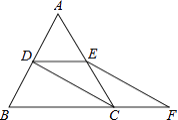
(1)求证:DE=CF;
(2)求EF的长.
参考答案:
【答案】
(1)证明:∵D、E分别为AB、AC的中点,
∴DE为△ABC的中位线,
∴DE ![]() BC,
BC,
∵延长BC至点F,使CF= ![]() BC,
BC,
∴DE=FC;
(2)解:∵DE ![]() FC,
FC,
∴四边形DEFC是平行四边形,
∴DC=EF,
∵D为AB的中点,等边△ABC的边长是2,
∴AD=BD=1,CD⊥AB,BC=2,
∴DC=EF= ![]() .
.
【解析】(1)直接利用三角形中位线定理得出DE ![]() BC,进而得出DE=FC;(2)利用平行四边形的判定与性质得出DC=EF,进而利用等边三角形的性质以及勾股定理得出EF的长.
BC,进而得出DE=FC;(2)利用平行四边形的判定与性质得出DC=EF,进而利用等边三角形的性质以及勾股定理得出EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司2012年缴税70万元,2014年缴税90万元,求该公司这两年缴税的年平均增长率.若设该公司这两年缴税的年平均增长率为x,根据题意,可得方程( )
A.70x2=90
B.70(1+x)2=90
C.70(1+x)=90
D.70+70(1+x)+70(1+x)2=90 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)(﹣4x2y3)(﹣ xyz)÷(
xyz)÷(  xy2)2
xy2)2
(2)(54x2y﹣108xy2﹣36xy)÷(18xy)
(3)(a+b+3)(a+b﹣3)
(4)20070+2﹣2﹣( )2+2014.
)2+2014. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.
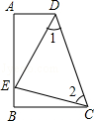
(1)求证:Rt△ADE与Rt△BEC全等;
(2)求证:△CDE是直角三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=
 (x>0)的图象与BC边交于点E.
(x>0)的图象与BC边交于点E.(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】若x+n与x+2的乘积中不含x的一次项,则n的值为( )
A.﹣2
B.2
C.0
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】把长为6厘米的线段水平向右平移10厘米后的新线段长为___________厘米
相关试题

