【题目】计算
(1)(﹣4x2y3)(﹣ ![]() xyz)÷(
xyz)÷( ![]() xy2)2
xy2)2
(2)(54x2y﹣108xy2﹣36xy)÷(18xy)
(3)(a+b+3)(a+b﹣3)
(4)20070+2﹣2﹣( ![]() )2+2014.
)2+2014.
参考答案:
【答案】
(1)解:(﹣4x2y3)(﹣ ![]() xyz)÷(
xyz)÷( ![]() xy2)2
xy2)2
=(﹣4x2y3)(﹣ ![]() xyz)÷(
xyz)÷( ![]() x2y4)
x2y4)
=2xz
(2)解:(54x2y﹣108xy2﹣36xy)÷(18xy)=3x﹣6y﹣2
(3)解:(a+b+3)(a+b﹣3)
=(a+b)2﹣9
=a2+2ab+b2﹣9
(4)解:20070+2﹣2﹣( ![]() )2+2014
)2+2014
=1+ ![]() ﹣
﹣ ![]() +2014
+2014
=2015
【解析】(1)先算积的乘方,再根据单项式的乘除法法则计算即可求解;(2)根据多项式除以单项式法则计算即可求解;(3)先根据平方差公式计算,再根据完全平方公式;(4)先算零指数幂,负整数指数幂,平方,再计算加减法即可求解.
【考点精析】掌握零指数幂法则和整数指数幂的运算性质是解答本题的根本,需要知道零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB∥CD,∠A=∠D,试说明 AC∥DE 成立的理由.
(下面是彬彬同学进行的推理,请你将彬彬同学的推理过程补充完整.)
解:∵AB∥CD (已知)
∴∠A=(两直线平行,内错角相等)
又∵∠A=∠D()
∴∠=∠(等量代换)
∴AC∥DE ()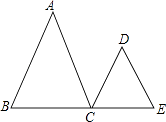
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,抛物线
 与
与 轴交于A、B(A点在B点的左侧)与
轴交于A、B(A点在B点的左侧)与 轴交于点C.
轴交于点C.(1)如图1,连接AC、BC,若△ABC的面积为3时,求抛物线的解析式;
(2)如图2,点P为第四象限抛物线上一点,连接PC,若
 时,求点P的横坐标;
时,求点P的横坐标;(3)如图3,在(2)的条件下,点F在AP上,过点P作PH⊥
 轴于H点,点K在PH的延长线上,AK=KF,∠KAH=∠FKH,PF=
轴于H点,点K在PH的延长线上,AK=KF,∠KAH=∠FKH,PF= ,连接KB并延长交抛物线于点Q,求PQ的长.
,连接KB并延长交抛物线于点Q,求PQ的长. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司2012年缴税70万元,2014年缴税90万元,求该公司这两年缴税的年平均增长率.若设该公司这两年缴税的年平均增长率为x,根据题意,可得方程( )
A.70x2=90
B.70(1+x)2=90
C.70(1+x)=90
D.70+70(1+x)+70(1+x)2=90 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.
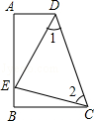
(1)求证:Rt△ADE与Rt△BEC全等;
(2)求证:△CDE是直角三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=
 BC,连接CD和EF.
BC,连接CD和EF. 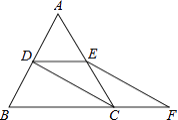
(1)求证:DE=CF;
(2)求EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=
 (x>0)的图象与BC边交于点E.
(x>0)的图象与BC边交于点E.(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?

相关试题

