【题目】时代中学从学生兴趣出发,实施体育活动课走班制.为了了解学生最喜欢的一种球类运动,以便合理安排活动场地,在全校至少喜欢一种球类(乒乓球、羽毛球、排球、篮球、足球)运动的1200名学生中,随机抽取了若干名学生进行调查(每人只能在这五种球类运动中选择一种).调查结果统计如下:
球类名称 | 乒乓球 | 羽毛球 | 排球 | 篮球 | 足球 |
人数 | 42 |
| 15 | 33 |
|
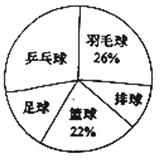
解答下列问题:
(1)这次抽样调查中的样本是________;
(2)统计表中,![]() ________,
________,![]() ________;
________;
(3)试估计上述1200名学生中最喜欢乒乓球运动的人数.
参考答案:
【答案】(1)时代中学学生最喜欢的一种球类运动情况;(2)39,21;(3)336人.
【解析】分析: (1)直接利用样本的定义分析得出答案;
(2)用喜欢排球的人数除以其所占的百分比即可求得样本容量,用样本容量乘以羽毛球所占的百分比即可求得a,用样本容量减去其他求得b值;
(3)用总人数乘以喜欢乒乓球的人所占的百分比即可.
详解:
(1)这次抽样调查中的样本是:时代中学学生最喜欢的一种球类运动情况;
故答案为:时代中学学生最喜欢的一种球类运动情况;
(2)∵喜欢蓝球的有33人,占22%,
∴样本容量为33÷22%=150;
a=150×26%=39(人),
b=150-39-42-15-33=21(人);
故答案为:39,21;
(3)最喜欢乒乓球运动的人数为:1200×![]() =336(人).
=336(人).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,平面直角坐标系中,抛物线y=ax2+bx+3与x轴的两个交点分别为A(﹣3,0),B(1,0),与y轴的交点为D,对称轴与抛物线交于点C,与x轴负半轴交于点H.

(1)求抛物线的表达式;
(2)点E,F分别是抛物线对称轴CH上的两个动点(点E在点F上方),且EF=1,求使四边形BDEF的周长最小时的点E,F坐标及最小值;
(3)如图2,点P为对称轴左侧,x轴上方的抛物线上的点,PQ⊥AC于点Q,是否存在这样的点P使△PCQ与△ACH相似?若存在请求出点P的坐标,若不存在请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OABC的两边OA,OC分别在x轴和y轴上,并且OA=5,OC=3.若把矩形OABC绕着点O逆时针旋转,使点A恰好落在BC边上的A1处,则点C的对应点C1的坐标为( )
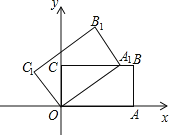
A. (﹣
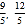 ) B. (﹣
) B. (﹣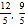 ) C. (﹣
) C. (﹣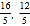 ) D. (﹣
) D. (﹣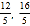 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】春季是传染病多发的季节,积极预防传染病是学校高度重视的一项工作,为此,某校对学生宿舍采取喷洒药物进行消毒.在对某宿舍进行消毒的过程中,先经过
 的集中药物喷洒,再封闭宿舍
的集中药物喷洒,再封闭宿舍 ,然后打开门窗进行通风,室内每立方米空气中含药量
,然后打开门窗进行通风,室内每立方米空气中含药量 与药物在空气中的持续时间
与药物在空气中的持续时间 之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比例,如图所示.下面四个选项中错误的是( )
之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比例,如图所示.下面四个选项中错误的是( )
A. 经过
 集中喷洒药物,室内空气中的含药量最高达到
集中喷洒药物,室内空气中的含药量最高达到
B. 室内空气中的含药量不低于
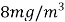 的持续时间达到了
的持续时间达到了
C. 当室内空气中的含药量不低于
 且持续时间不低于35分钟,才能有效杀灭某种传染病毒.此次消毒完全有效
且持续时间不低于35分钟,才能有效杀灭某种传染病毒.此次消毒完全有效D. 当室内空气中的含药量低于
 时,对人体才是安全的,所以从室内空气中的含药量达到
时,对人体才是安全的,所以从室内空气中的含药量达到 开始,需经过
开始,需经过 后,学生才能进入室内
后,学生才能进入室内 -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司在甲、乙两座仓库分别有农用车
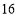 辆和
辆和 辆,现需要调往
辆,现需要调往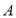 县
县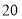 辆, 调往
辆, 调往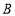 县
县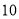 辆,已知从甲仓库调运一辆农用车到
辆,已知从甲仓库调运一辆农用车到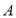 县和
县和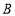 县的运费分别为
县的运费分别为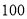 元和
元和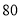 元,从乙仓库调运一辆农用车到
元,从乙仓库调运一辆农用车到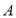 县和
县和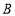 县的运费分别为
县的运费分别为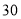 元和
元和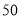 元,从甲仓库调往
元,从甲仓库调往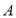 县农用车
县农用车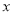 辆.
辆.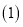 甲仓库调往
甲仓库调往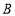 县农用车____ 辆,乙仓库调往
县农用车____ 辆,乙仓库调往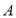 县农用车 _辆、乙仓库调往B县农用车____ 辆(用含
县农用车 _辆、乙仓库调往B县农用车____ 辆(用含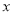 的代数式表示);
的代数式表示);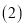 写出公司从甲、乙两座仓库调农用车到
写出公司从甲、乙两座仓库调农用车到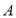 、
、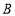 两县所需要的总运费(用含
两县所需要的总运费(用含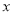 的代数式表示);
的代数式表示);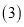 在
在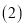 的基础上,求当总运费是
的基础上,求当总运费是元时,从甲仓库调往
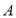 县农用车多少辆?
县农用车多少辆? -
科目: 来源: 题型:
查看答案和解析>>【题目】小淇在说明 “直角三角形斜边上的中线等于斜边的一半”是真命题,部分思路如下:如图,在∠ACB内做∠BCD=∠B,CD与AB相交于点D,…….请根据以上思路,完成证明.

-
科目: 来源: 题型:
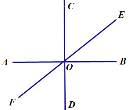
查看答案和解析>>【题目】如图,直线AB、CD、EF相交于点O,且∠AOC=90°,∠AOE=140°,
(1)直线AB与直线______垂直,记作______;
(2)直线AB与直线______斜交,夹角的大小为______;
(3)直线_____与直线______夹角的大小为50°.
相关试题

