【题目】“校园手机”现象越来越受到社会的关注.小丽在“统计实习”活动中随机调查了学校若干名学生家长对“中学生带手机到学校”现象的看法,统计整理并制作了如下的统计图: 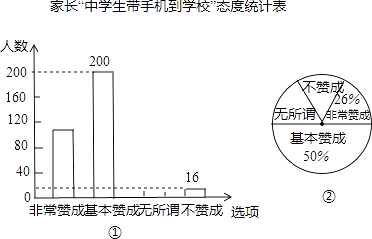
(1)求这次调查的家长总数及家长表示“无所谓”的人数,并补全图①;
(2)求图②中表示家长“无所谓”的圆心角的度数;
(3)从这次接受调查的家长中,随机抽查一个,恰好是“不赞成”态度的家长的概率是多少.
参考答案:
【答案】
(1)解:家长总数:200÷50%=400名,
表示“无所谓”人数:400﹣200﹣16﹣400×26%=80名,补全图①, 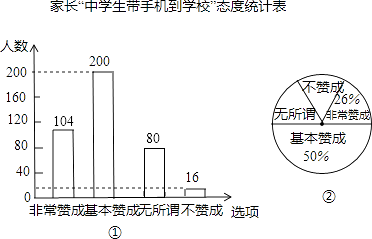
(2)解:80÷400×360°=72°
(3)解:16÷400= ![]()
【解析】(1)由图象可以得出基本赞成的有200人占50%,可以求出总数,由总数可以求出非常赞成的人数和无所谓的人数.(2)由(1)的总数求出无所谓的百分比再乘以360°就可以求出圆心角的度数.(3)这次受调查的家长不赞成的人数除以总数就是抽到恰好是“不赞成”态度的家长的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论中:①abc>0;②2a+b<0;③a+b<m(am+b)(m≠1的实数);④(a+c)2<b2;⑤a>1.其中正确的项是( )
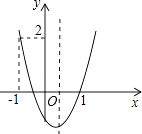
A.①⑤
B.①②⑤
C.②⑤
D.①③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】下面图形:四边形,三角形,梯形,平行四边形,菱形,矩形,正方形,圆,从中任取一个图形既是轴对称图形又是中心对称图形的概率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年入春以来,湖南省大部分地区发生了罕见的旱灾,连续几个月无有效降水.为抗旱救灾,驻湘某部计划为驻地村民新建水渠3600米,为使水渠能尽快投入使用,实际工作效率是原计划工作效率的1.8倍,结果提前20天完成修水渠任务.问原计划每天修水渠多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形、菱形、正方形都是平行四边形,但它们都是有特殊条件的平行四边形,正方形不仅是特殊的矩形,也是特殊的菱形.因此,我们可利用矩形、菱形的性质来研究正方形的有关问题.回答下列问题:

(1)将平行四边形、矩形、菱形、正方形填入它们的包含关系的下图中.
(2)要证明一个四边形是正方形,可先证明四边形是矩形,再证明这个矩形的相等;或者先证明四边形是菱形,在证明这个菱形有一个角是 .
(3)某同学根据菱形面积计算公式推导出对角线长为a的正方形面积是S=0.5a2 , 对此结论,你认为是否正确?若正确,请说明理由;若不正确,请举出一个反例说明. -
科目: 来源: 题型:
查看答案和解析>>【题目】2011年3月11日13时46分日本发生了9.0级大地震,伴随着就是海啸.山坡上有一颗与水平面垂直的大树,海啸过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示).已知山坡的坡角∠AEF=23°,测得树干的倾斜角为∠BAC=38°,大树被折断部分和坡面的角∠ADC=60°,AD=4米.

(1)求∠DAC的度数;
(2)求这棵大树折断前高是多少米?(注:结果精确到个位)(参考数据: )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点M,连接OM,过点M作⊙O的切线交边BC于N.

(1)求证:△ODM∽△MCN;
(2)设DM=x,求OA的长(用含x的代数式表示);
(3)在点O的运动过程中,设△CMN的周长为P,试用含x的代数式表示P,你能发现怎样的结论?
相关试题

