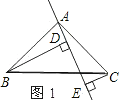
【题目】(1)如图1,△ABC中,∠BAC=90°,AB=AC,AE是过A点的一条直线,且B、C在AE的异侧,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE.
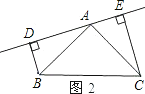
(2)若直线AE绕点A旋转到图2的位置时(BD<CE),其余条件不变,问BD与DE、CE的关系如何?请予以证明.


参考答案:
【答案】见解析
【解析】
试题分析:根据已知利用AAS判定△ABD≌△CAE从而得到BD=AE,AD=CE,因为AE=AD+DE,所以BD=DE+CE;
根据已知利用AAS判定△ABD≌△CAE从而得到BD=AE,AD=CE,因为AD+AE=BD+CE,所以BD=DE﹣CE.
解:(1)∵∠BAC=90°,BD⊥AE,CE⊥AE,
∴∠BDA=∠AEC=90°,
∵∠ABD+∠BAE=90°,∠CAE+∠BAE=90°
∴∠ABD=∠CAE,
∵AB=AC,
在△ABD和△CAE中,
∵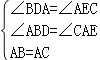 ,
,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AE=AD+DE,
∴BD=DE+CE;
(2)BD=DE﹣CE;
∵∠BAC=90°,BD⊥AE,CE⊥AE,
∴∠BDA=∠AEC=90°,
∵AB=AC,
在△ABD和△CAE中,
∵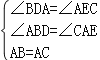 ,
,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∴AD+AE=BD+CE,
∵DE=BD+CE,
∴BD=DE﹣CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任两螺丝间距离的最大值为( )
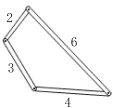
A.5 B.6 C.7 D.10
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. a2+a3=2a5 B. a6÷a2=a3
C. a2a3=a5 D. (2ab2)3=6a3b6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A→C→B路径向终点运动,终点为B点;点Q从B点出发沿B→C→A路径向终点运动,终点为A点.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.设运动时间为t秒,则当t=_________秒时,△PEC与△QFC全等.
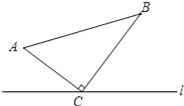
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=2x2向左平移1个单位,再向下平移2个单位,得到的抛物线是( )
A.y=2(x+1)2+2
B.y=2(x﹣1)2+2
C.y=2(x﹣1)2﹣2
D.y=2(x+1)2﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】定义一种新运算“⊕”,其运算规则为:a⊕b=﹣2a+3b,如:1⊕5=(﹣2)×1+3×5=13,则方程x⊕2=0的解为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2﹣2x=0的根是( )
A.x1=0,x2=﹣2
B.x1=0,x2=2
C.x=0
D.x=2
相关试题

