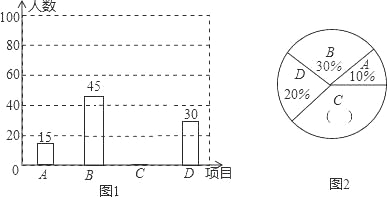
【题目】为进一步推广“阳光体育”大课间活动,某中学对已开设的A实心球,B立定跳远,C跑步,D跳绳四种活动项目的学生喜欢情况进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2的统计图,请结合图中的信息解答下列问题:
(1)请计算本次调查中喜欢“跑步”的学生人数和所占百分比,并将两个统计图补充完整;
(2)随机抽取了5名喜欢“跑步”的学生,其中有3名女生,2名男生,现从这5名学生中任意抽取2名学生,请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.
参考答案:
【答案】(1)60人;40%;(2)
【解析】试题分析:(1)用A的人数除以所占的百分比,即可求出调查的学生数;用抽查的总人数减去A、B、D的人数,求出喜欢“跑步”的学生人数,再除以被调查的学生数,求出所占的百分比,再画图即可;
(2)用A表示男生,B表示女生,画出树形图,再根据概率公式进行计算即可.
试题解析:(1)根据题意得:
15÷10%=150(名).
本项调查中喜欢“跑步”的学生人数是;150-15-45-30=60(人),
所占百分比是: ![]() ×100%=40%,
×100%=40%,
画图如下:

(2)用A表示男生,B表示女生,画图如下:

共有20种情况,同性别学生的情况是8种,
则刚好抽到同性别学生的概率是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题是( ) .
A. 对角线相等的四边形是矩形;
B. 对角线互相垂直的四边形是菱形;
C. 对角线互相平分的四边形是平行四边形;
D. 对角线互相垂直平分的四边形是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=- (x-2)2+7,当m≤x≤n且mn<0时,y的最小值为2m,最大值为2n,则m+n的值为( )
A. 2 B.
 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】有两个一元二次方程:M:ax2+bx+c=0,N:cx2+bx+a=0,其中a+c=0,以下列四个结论中正确的是_____(填写序号).
①如果方程M有两个不相等的实数根,那么方程N也有两个不相等的实数根;
②如果方程M有两根符号相同,那么方程N的两根符号也相同;
③如果方程M和方程N有一个相同的根,那么这个根必是x=1;
④如果5是方程M的一个根,那么
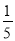 是方程N的一个根.
是方程N的一个根. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为E.
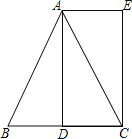
(1)求证:△ABD≌△CAE;
(2)连接DE,线段DE与AB之间有怎样的位置和数量关系?请证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
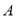 在数轴上对应的数为
在数轴上对应的数为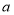 ,点
,点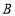 对应的数为
对应的数为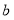 ,
,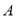 与
与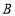 之间的距离记作AB.
之间的距离记作AB.
已知a=-2,b比a大12,(1)则B点表示的数是_____;
(2)设点
 在数轴上对应的数为
在数轴上对应的数为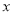 ,当PA-PB=4时,求
,当PA-PB=4时,求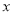 的值;
的值;(3)若点M以每秒1个单位的速度从A点出发向右运动,同时点N以每秒2个单位的速度从B点向左运动。设运动时间是t秒,则运动t秒后,
用含t的代数式表示M点到达的位置表示的数为_____, N点到达的位置表示的数为_____;
当t为多少秒时,M与N之间的距离是9?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=45°,AD⊥BC于点D,BE⊥AC于点E,点F是AB的中点, AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;② AH=2BD; ③AD·BC=AE·AB; ④2CD2=
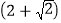 EH2.其中正确的结论有( )
EH2.其中正确的结论有( )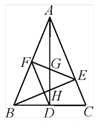
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

