Question

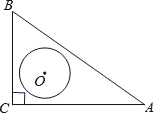
【题目】如图，在Rt△ABC中，∠C=90°，AC=4，BC=3，O是△ABC的内心，以O为圆心，r为半径的圆与线段AB有公共点，则r的取值范围是_____．

Answer 1

【答案】1≤r≤

【解析】分析：作OD⊥AB于D，OE⊥BC于E，OF⊥AC于F，根据题意得出四边形OECF是正方形，得出OF=CF，由勾股定理得出AB==5，由内心的性质得出CF=OF=1，AF=AC﹣CF=3，由勾股定理求出OA，由直线与圆的位置关系，即可得出结果．

详解：作OD⊥AB于D，OE⊥BC于E，OF⊥AC于F，连接OA、OB，如图所示

则四边形OECF是正方形，∴OF=CF=OE=CE．

∵∠C=90°，AC=4，BC=3，∴AB==5．

∵O是△ABC的内心，∴CE=CF=OF=OE=（AC+BC﹣AB）=1，∴AF=AC﹣CF=3，BE=BC﹣CE=2，∴OA===，OB===，当r=1时，以O为圆心，r为半径的圆与线段AB有唯一交点；

当1＜r≤时，以O为圆心，r为半径的圆与线段AB有两个交点；

当＜r≤时，以O为圆心，r为半径的圆与线段AB有1个交点；

∴以O为圆心，r为半径的圆与线段AB有交点，则r的取值范围是1≤r≤；

故答案为：1≤r≤．