【题目】如图,抛物线y=x2![]() 2x+c的顶点A在直线l:y=x
2x+c的顶点A在直线l:y=x![]() 5上.
5上.
(1)求抛物线顶点A的坐标;
(2)设抛物线与y轴交于点B,与x轴交于点C、D(C点在D点的左侧),试判断△ABD的形状;
(3)在直线l上是否存在一点P,使以点P、A、B、D为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)A(1,﹣4);
(2)△ABD是直角三角形,理由见解析;
(3)存在点P(﹣2,﹣7)或P(4,﹣1),使以点A、B、D、P为顶点的四边形是平行四边形.
【解析】试题分析:(1)先根据抛物线的解析式得出其对称轴方程,由此得到顶点A的横坐标,然后代入直线l的解析式中即可求出点A的坐标.
(2)由A点坐标可确定抛物线的解析式,进而可得到点B的坐标.则AB、AD、BD三边的长可得,然后根据边长确定三角形的形状.
(3)若以点P、A、B、D为顶点的四边形是平行四边形,应分①AB为对角线、②AD为对角线两种情况讨论,然后结合勾股定理以及边长的等量关系列方程求出P点的坐标.
(1)∵顶点A的横坐标为![]() ,且顶点在y=x﹣5上,
,且顶点在y=x﹣5上,
∴当x=1时,y=1-5=-4,
∴A(1,-4).
(2)将A(1,-4)代入y=x2-2x+c,可得,1-2+c=-4,c=-3,
∴y=x2-2x-3,
∴B(0,-3)
当y=0时,x2-2x-3=0,x1=-1,x2=3
∴C(-1,0),D(3,0),
∵BD2=OB2+OD2=18,AB2=(4-3)2+12=2,AD2=(3-1)2+42=20,
∴BD2+AB2=AD2,
∴∠ABD=90°,即△ABD是直角三角形.
(3)由题意知:直线y=x-5交y轴于点E(0,-5),交x轴于点F(5,0)
∴OE=OF=5,
又∵OB=OD=3
∴△OEF与△OBD都是等腰直角三角形
∴BD∥l,即PA∥BD
则构成平行四边形只能是PADB或PABD,如图,
过点P作y轴的垂线,过点A作x轴的垂线交过P且平行于x轴的直线于点G.
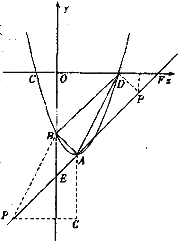
设P(x1,x1-5),则G(1,x1-5)
则PG=|1-x1|,AG=|5-x1-4|=|1-x1|
PA=BD=3![]()
由勾股定理得:
(1-x1)2+(1-x1)2=18,x12-2x1-8=0,x1=-2或4
∴P(-2,-7)或P(4,-1),
存在点P(-2,-7)或P(4,-1)使以点A、B、D、P为顶点的四边形是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为积极响应“弘扬传统文化”的号召,某学校组织全校1200名学生进行经典诗词诵读活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取40名学生调查“一周诗词诵背数量”,根据调查结果绘制成的统计图如图所示.

大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表如下:
一周诗词诵背数量
3首
4首
5首
6首
7首
8首
人数
1
3
5
6
10
15
请根据调查的信息
(1)求活动启动之初学生“一周诗词诵背数量”的中位数;
(2)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
(3)选择适当的统计量,至少从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究题:如图,用同样大小的黑色棋子按如图所示的规律摆放,它们的棋子数依次表示为 a1,a2,a3,a4,…,an.
 …
… 请你认真观察上面四个图案,从中发现规律,并试着解答下列问题:
(1)写出 a1,a2,a3,a4 的值;
(2)求 a7 的值;
(3)用 n 表示出 an,并判断第几个图案有 6055 个黑色棋子.
-
科目: 来源: 题型:
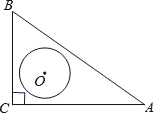
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,O是△ABC的内心,以O为圆心,r为半径的圆与线段AB有公共点,则r的取值范围是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)
(1)画出△ABC向下平移4个单位,再向左平移1个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)作出△ABC绕点A顺时针方向旋转90°后得到的△A2B2C2,并直接写出C2点的坐标;

-
科目: 来源: 题型:
查看答案和解析>>【题目】图
 是一个可以自由转动的转盘,被分成了面积相等的三个扇形,分别标有数
是一个可以自由转动的转盘,被分成了面积相等的三个扇形,分别标有数 ,
,  ,
,  ,甲转动一次转盘,转盘停止后指针指向的扇形内的数记为
,甲转动一次转盘,转盘停止后指针指向的扇形内的数记为 (如果指针恰好指在分割线上,那么重转一次,直到指针指向某一扇形为止).图
(如果指针恰好指在分割线上,那么重转一次,直到指针指向某一扇形为止).图 是背面完全一样、牌面数字分别是
是背面完全一样、牌面数字分别是 ,
,  ,
,  ,
,  的四张扑克牌,把四张扑克牌背面朝上,洗匀后放在桌面上,乙随机抽出一张牌的牌面数字记为
的四张扑克牌,把四张扑克牌背面朝上,洗匀后放在桌面上,乙随机抽出一张牌的牌面数字记为 .计算
.计算 的值.
的值.

(
 )用树状图或列表法求
)用树状图或列表法求 的概率.
的概率.(
 )甲乙两人玩游戏,规定:当
)甲乙两人玩游戏,规定:当 是正数时,甲胜;否则,乙胜,你认为这个游戏规则对甲乙双方公平吗?请说明理由.
是正数时,甲胜;否则,乙胜,你认为这个游戏规则对甲乙双方公平吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】为拓宽学生视野,引导学生主动适应社会,促进书本知识和生活经验的深度融合,我市某中学决定组织部分班级去赤壁开展研学旅行活动,在参加此次活动的师生中,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生.现有甲、乙两种大客车,它们的载客量和租金如表所示.
甲种客车
乙种客车
载客量/(人/辆)
30
42
租金/(元/辆)
300
400
学校计划此次研学旅行活动的租车总费用不超过3100元,为了安全,每辆客车上至少要有2名老师.
(1)参加此次研学旅行活动的老师和学生各有多少人?
(2)既要保证所有师生都有车坐,又要保证每辆客车上至少要有2名老师,可知租用客车总数为 辆;
(3)你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.
相关试题

