Question

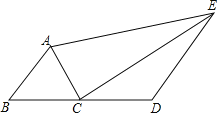
【题目】如图，在四边形ABDE中，C是BD边的中点．若AC平分∠BAE，∠ACE=90°，猜想线段AE、AB、DE的长度满足的数量关系为并证明．

Answer 1

【答案】AE=AB+DE．

【解析】

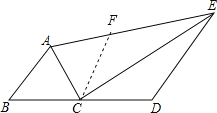
试题分析：在AE上取一点F，使AF=AB，即可得出△ACB≌△ACF，就可以得出BC=FC，∠ACB=∠ACF，就可以得出△CEF≌△CED．就可以得出结论．

解：AE=AB+DE；

理由：在AE上取一点F，使AF=AB．

∵AC平分∠BAE，

∴∠BAC=∠FAC．

在△ACB和△ACF中，

，

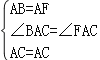∴△ACB≌△ACF（SAS），

∴BC=FC，∠ACB=∠ACF．

∵C是BD边的中点．

∴BC=CD，

∴CF=CD．

∵∠ACE=90°，

∴∠ACB+∠DCE=90°，∠ACF+∠ECF=90°

∴∠ECF=∠ECD．

在△CEF和△CED中，

，

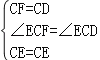∴△CEF≌△CED（SAS），

∴EF=ED．

∵AE=AF+EF，

∴AE=AB+DE．