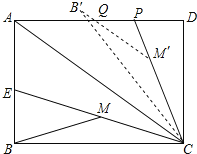
【题目】已知矩形ABCD中,AB=3,BC=4,CE平分∠ACB交AB于点E,M为CE的中点,连结BM,将△BCM绕点C顺时针旋转至△B′CM′,B′M′交AD于Q,延长CM′交AD于P,若PQ=PM′,则PQ= .
参考答案:
【答案】![]() ﹣
﹣![]() .
.
【解析】
试题分析:首先证明四边形ACM'Q是等腰梯形,设PQ=x,在直角△CDP中,根据勾股定理即可得到关于x的方程求得x的值.
解:设PQ=x,
∵CE平分∠ACB,
∴∠BCE=∠ACE,且![]() =
=![]() ,
,
∵AB=3,BC=4,
∴AC=5,
∴![]() ,
,
∴BE=![]() ,AE=
,AE=![]() ,
,
∴CE=![]() ,
,
∴CM=![]() .
.
∵M是CE的中点,且△BCE是直角三角形,
∴BM=CM=EM,
∴∠CBM=∠BCM=∠ACE,
又△B'CM'是△BCM旋转得到,
∴△B'CM'≌△BCM.
∵PQ=P'M,
∴∠PM'Q=∠PQM'=2∠B'CM'=∠ACB.
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ACB=∠CAD,
∴∠PQM'=CAD,
∴AC∥B'M',
∴∠PM'Q=∠ACP,
∴∠CAD=∠ACP,
∴四边形ACM'Q是等腰梯形,
∴AQ=CM'=![]() ,
,
∴PD=![]() +x,
+x,
在直角△CDP中,根据勾股定理得:CP2=PD2+CD2,
(![]() +x)2=(4﹣
+x)2=(4﹣![]() ﹣x)2+9,另t=
﹣x)2+9,另t=![]() +x,则t2=(4﹣t)2+9,
+x,则t2=(4﹣t)2+9,
∴t=![]() ,
,
∴![]() +x=
+x=![]() ,
,
∴x=![]() ﹣
﹣![]() ,
,
∴PQ=![]() ﹣
﹣![]() .
.
故答案是:![]() ﹣
﹣![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,将一个圆依次二等分、三等分、四等分、五等分…,并按图中规律在半径上摆放黑色棋子,则第一幅图中有5个棋子,第二幅图中有10个棋子,第三幅图中有17个棋子,第四幅图中有26个棋子,依此规律,则第6幅图中所含棋子数目为( )

A.51 B.50 C.49 D.48
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x,纵坐标y的对应值如表:
x
…
﹣1
0
1
2
3
4
…
y
…
﹣

1
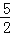
3
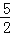
1
…
从上表可知,下列说法错误的是( )
A.对称轴为直线x=2
B.图象开口向下
C.顶点坐标(2,3)
D.当x=5时,y=
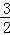
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个一次函数的图象平行于直线y=-2x,且过点A(-4,2),求这个函数的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果两个相似三角形的面积比是1:4,那么它们的周长比是( )
A.1:16 B.1:4 C.1:6 D.1:2
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程(a﹣1)x2+x+a2﹣1=0的一个根是0,则a的值是( )
A.﹣1 B.1 C.1或﹣1 D.﹣1或0
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解.
(1)2a2﹣2; (2)m2﹣12mn+36n2.
相关试题

