【题目】已知,m,n是一元二次方程![]() 的两个实数根,且|m|<|n|,抛物线
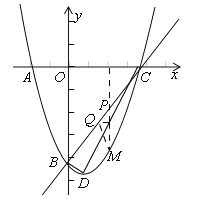
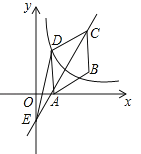
的两个实数根,且|m|<|n|,抛物线![]() 的图象经过点A(m,0),B(0,n),如图所示.
的图象经过点A(m,0),B(0,n),如图所示.
(1)求这个抛物线的解析式;
(2)设(1)中的抛物线与x轴的另一个交点为抛物线的顶点为D,试求出点C,D的坐标,并判断△BCD的形状;
(3)点P是直线BC上的一个动点(点P不与点B和点C重合),过点P作x轴的垂线,交抛物线于点M,点Q在直线BC上,距离点P为![]() 个单位长度,设点P的横坐标为t,△PMQ的面积为S,求出S与t之间的函数关系式.
个单位长度,设点P的横坐标为t,△PMQ的面积为S,求出S与t之间的函数关系式.

参考答案:
【答案】(1)![]() ;(2)△BCD是直角三角形;(3)S=
;(2)△BCD是直角三角形;(3)S=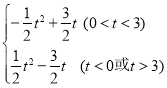 .
.
【解析】
试题分析:(1)先解一元二次方程,然后用待定系数法求出抛物线解析式;
(2)先解方程求出抛物线与x轴的交点,再判断出△BOC和△BED都是等腰直角三角形,从而得到结论;
(3)先求出QF=1,再分两种情况,当点P在点M上方和下方,分别计算即可.
试题解析:解(1)∵![]() ,∴
,∴![]() ,
,![]() ,∵m,n是一元二次方程
,∵m,n是一元二次方程![]() 的两个实数根,且|m|<|n|,∴m=﹣1,n=﹣3,∵抛物线
的两个实数根,且|m|<|n|,∴m=﹣1,n=﹣3,∵抛物线![]() 的图象经过点A(m,0),B(0,n),∴
的图象经过点A(m,0),B(0,n),∴![]() ,∴
,∴![]() ,∴抛物线解析式为
,∴抛物线解析式为![]() ;
;
(2)令y=0,则![]() ,∴
,∴![]() ,
,![]() ,∴C(3,0),∵
,∴C(3,0),∵![]() =
=![]() ,∴顶点坐标D(1,﹣4),过点D作DE⊥y轴,∵OB=OC=3,∴BE=DE=1,∴△BOC和△BED都是等腰直角三角形,∴∠OBC=∠DBE=45°,∴∠CBD=90°,∴△BCD是直角三角形;
,∴顶点坐标D(1,﹣4),过点D作DE⊥y轴,∵OB=OC=3,∴BE=DE=1,∴△BOC和△BED都是等腰直角三角形,∴∠OBC=∠DBE=45°,∴∠CBD=90°,∴△BCD是直角三角形;
(3)如图,∵B(0,﹣3),C(3,0),∴直线BC解析式为y=x﹣3,∵点P的横坐标为t,PM⊥x轴,∴点M的横坐标为t,∵点P在直线BC上,点M在抛物线上,∴P(t,t﹣3),M(t,![]() ),过点Q作QF⊥PM,∴△PQF是等腰直角三角形,∵PQ=
),过点Q作QF⊥PM,∴△PQF是等腰直角三角形,∵PQ=![]() ,∴QF=1.
,∴QF=1.
①当点P在点M上方时,即0<t<3时,PM=t﹣3﹣(![]() )=
)=![]() ,∴S=
,∴S=![]() PM×QF=
PM×QF=![]() =
=![]() ,②如图3,当点P在点M下方时,即t<0或t>3时,PM=
,②如图3,当点P在点M下方时,即t<0或t>3时,PM=![]() ﹣(t﹣3)=
﹣(t﹣3)=![]() ,∴S=
,∴S=![]() PM×QF=
PM×QF=![]() (
(![]() )=
)=![]() .
.
综上所述,S=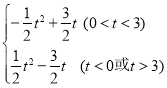 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形的一个内角是80°,则它的顶角是 °.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若7名学生的体重(单位:kg)分别是:40,42,43,45,47,47,58,则这组数据的平均数是( )
A.44
B.45
C.46
D.47 -
科目: 来源: 题型:
查看答案和解析>>【题目】化简(3m+2)﹣3(m2﹣m+1)+(3﹣6m).
-
科目: 来源: 题型:
查看答案和解析>>【题目】若m2﹣2m﹣1=0,则代数式2m2﹣4m+3的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=(x+3)2﹣4,将其图象沿y轴向下平移1个单位,再沿x轴向左平移2个单位,则该抛物线的解析式为( )
A. y=(x+5)2 ﹣5B. y=( x+1)2 ﹣3
C. y=( x+1) 2 ﹣5D. y=( x+5) 2 ﹣3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点A、B、C的坐标分别是(1,0)、(3,1)、(3,3),双曲线
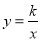 (k≠0,x>0)过点D.
(k≠0,x>0)过点D.(1)求双曲线的解析式;
(2)作直线AC交y轴于点E,连结DE,求△CDE的面积.
相关试题

