【题目】(1)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,AD⊥MN于点D,BE⊥MN于点E,当直线MN旋转到图1的位置时,求证:DE=AD+BE;
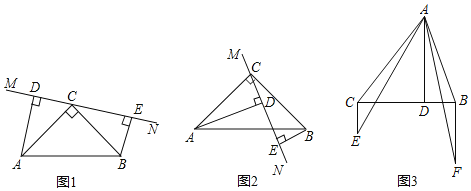
(2)在(1)的条件下,当直线MN旋转到图2的位置时,猜想线段AD,DE,BE的数量关系,并证明你的猜想;
(3)如图3,在△ABC中,AD⊥BC于D,AD=BC,BF⊥BC于B,BF=CD,CE⊥BC于C,CE=BD,求证:∠EAF+∠BAC=90°.
参考答案:
【答案】(1)见解析;(2)DE=AD﹣BE,证明见解析;(3)见解析.
【解析】
(1)由已知条件可推出∠ACD=∠CBE,继而可证明△ADC≌△CEB,利用全等三角形的性质可证明结论;
(2)与(1)证法类似,可推出∠ACD=∠CBE,证明△ADC≌△CEB,得出AD=CE,DC=BE,继而得出结论;
(3)连接CF、BE,可证明△ADC≌△CBF,进一步推出△ACF为等腰直角三角形,同理可推出△ABE为等腰直角三角形,从而可得出结论.
解:(1)证明:∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
而AD⊥MN于D,BE⊥MN于E,
∴∠ADC=∠CEB=90°,
∴∠BCE+∠CBE=90°,
∴∠ACD=∠CBE,
在△ADC和△CEB中, ,
,
∴△ADC≌△CEB(AAS),
∴AD=CE,DC=BE,
∴DE=DC+CE=BE+AD;
(2)DE=AD﹣BE,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
而AD⊥MN于D,BE⊥MN于E,
∴∠ADC=∠CEB=90°,
∴∠BCE+∠CBE=90°,
∴∠ACD=∠CBE,
在△ADC和△CEB中, ,
,
∴△ADC≌△CEB(AAS),
∴AD=CE,DC=BE,
∴DE=CE﹣CD=AD﹣BE;
(3)如图3,连接CF、BE,
AD⊥BC于D,BF⊥BC于B,
∴∠ADC=∠CBF=90°,
在△ADC和△CBF中,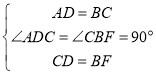 ,
,
∵△ADC≌△CBF(SAS),
∴∠CAD=∠FCB,AC=CF;
∴∠ACF=∠FCB+∠ACD=∠CAD+∠ACD=∠ADC=90°
∴△ACF为等腰直角三角形.
∴∠CAF=45°,
同理:△ABE为等腰直角三角形.
∴∠EAB=45°,
∴∠EAF+∠BAC=∠CAF+∠EAB=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )

A. OE=
 DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE -
科目: 来源: 题型:
查看答案和解析>>【题目】某市公交公司为应对春运期间的人流高峰,计划购买A、B两种型号的公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车3辆,共需650万元,
(1)试问该公交公司计划购买A型和B型公交车每辆各需多少万元?
(2)若该公司预计在某条线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用W不超过1200万元,且确保这10辆公交车在某条线路的年均载客量总和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案的总费用W最少?最少总费用是多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】七(一)班同学为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据整理如下表(部分):若该小区有
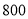 户家庭,据此估计该小区月均用水量不超过
户家庭,据此估计该小区月均用水量不超过 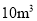 的家庭约有
的家庭约有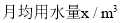
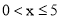
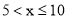
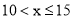
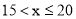
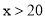
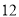
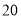
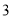
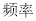
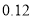
-
科目: 来源: 题型:
查看答案和解析>>【题目】分别从两个班级中随意抽取甲、乙两组各10名学生,他们的数学测验成绩(单位:分)如下:

计算甲、乙两组学生数学测验成绩的平均数、标准差和方差,哪个班级学生的成绩比较整齐?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,A、B两个旅游点从2010年至2014年“五、一”的旅游人数变化情况分别用实线和虚线表示.根据图中所示解答以下问题:

(1)B旅游点的旅游人数相对上一年,增长最快的是哪一年?
(2)求A、B两个旅游点从2010到2014年旅游人数的平均数和方差,并从平均数和方差的角度,用一句话对这两个旅游点的情况进行评价.
-
科目: 来源: 题型:
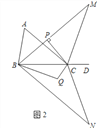
查看答案和解析>>【题目】如图1,点D为△ABC边BC的延长线上一点.

(1)若∠A∶∠ABC=3∶4,∠ACD=140°,求∠A的度数;
(2)若∠ABC的角平分线与∠ACD的角平分线交于点M,过点C作CP⊥BM于点P.
求证:
 ;
;(3)在(2)的条件下,将△MBC以直线BC为对称轴翻折得到△NBC,∠NBC的角平分线与∠NCB的角平分线交于点Q(如图2),试探究∠BQC与∠A有怎样的数量关系,请写出你的猜想并证明.
相关试题

