【题目】如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两地之间修建一条笔直的公路. 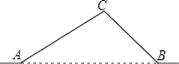
(1)求改直的公路AB的长;
(2)问公路改直后比原来缩短了多少千米?(sin25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75)
参考答案:
【答案】
(1)解:作CH⊥AB于H.
在Rt△ACH中,CH=ACsin∠CAB=ACsin25°≈10×0.42=4.2(千米),
AH=ACcos∠CAB=ACcos25°≈10×0.91=9.1(千米),
在Rt△BCH中,BH=CH÷tan∠CBA=4.2÷tan37°≈4.2÷0.75=5.6(千米),
∴AB=AH+BH=9.1+5.6=14.7(千米).
故改直的公路AB的长14.7千米
(2)解:在Rt△BCH中,BC=CH÷sin∠CBA=4.2÷sin37°≈4.2÷0.6=7(千米),
则AC+BC﹣AB=10+7﹣14.7=2.3(千米).
答:公路改直后比原来缩短了2.3千米.
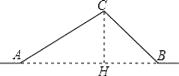
【解析】(1)作CH⊥AB于H.在Rt△ACH中,根据三角函数求得CH,AH,在Rt△BCH中,根据三角函数求得BH,再根据AB=AH+BH即可求解;(2)在Rt△BCH中,根据三角函数求得BC,再根据AC+BC﹣AB列式计算即可求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装销售店到生产厂家选购A、B两种品牌的服装,若购进A品牌服装3套,B品牌服装4套,共需600元;若购进A品牌服装2套,B品牌服装3套,共需425元.
(1)求A、B两种品牌的服装每套进价分别为多少元?
(2)若A品牌服装每套售价为130元,B品牌服装每套售价为100元,根据市场的需求,现决定购进B品牌服装数量比A品牌服装数量的2倍还多3套.如果购进B品牌服装数量不多于39套,这样服装全部售出后,就能使获利总额不少于1335元,问共有几种进货方案?如何进货?(注:利润=售价-进价)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆客车从甲地开往乙地,一辆轿车从乙地开往甲地,两车同时出发,两车行驶x小时后,记客车离甲地的距离为y1千米,轿车离甲地的距离为y2千米,y1、y2关于x的函数图象如图.
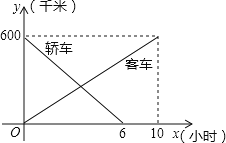
(1)根据图象,直接写出y1、y2关于x的函数关系式;
(2)当两车相遇时,求此时客车行驶的时间;
(3)两车相距200千米时,求客车行驶的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图图案是用长度相同的火柴棒按一定规律拼搭而成,图案①需8根火柴棒,图案②需15根火柴棒,…,

(1)按此规律,图案⑦需____根火柴棒;第n个图案需____根火柴棒.
(2)用2018根火柴棒能按规律拼搭而成一个图案?若能,说明是第几个图案:若不可能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线 l1 经过点 A(5,0)和点 B(
 ,﹣5)
,﹣5)(1)求直线 l1 的表达式;
(2)设直线 l2 的解析式为 y=﹣2x+2,且 l2 与 x 轴交于点 D,直线 l1 交 l2 于点 C, 求△CAD 的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)叙述并证明三角形内角和定理(证明用图 1);
(2)如图 2 是七角星形,求∠A+∠B+∠C+∠D+∠E+∠F+∠G 的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】大润发超市在销售某种进货价为20元/件的商品时,以30元/件售出,每天能售出100件.调查表明:这种商品的售价每上涨1元/件,其销售量就将减少2件.
(1)为了实现每天1600元的销售利润,超市应将这种商品的售价定为多少?
(2)设每件商品的售价为x元,超市所获利润为y元. ①求y与x之间的函数关系式;
②物价局规定该商品的售价不能超过40元/件,超市为了获得最大的利润,应将该商品售价定为多少?最大利润是多少?
相关试题

