搜索
【题目】如图，在平面直角坐标系网格中，△ABC的顶点都在格点上，点C坐标（0，﹣1）．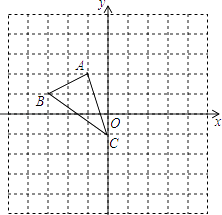
（1）作出△ABC关于原点对称的△A1B1C1 ， 并写出点A1的坐标；
（2）把△ABC绕点C逆时针旋转90°，得△A2B2C，画出△A2B2C，并写出点A2的坐标；
（3）直接写出△A2B2C的面积．
参考答案：
【答案】
（1）
解：如图所示：
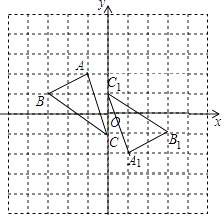
点A1的坐标为：（1，﹣2）；
（2）
解：如图所示：点A2的坐标为：（﹣3，﹣2）；
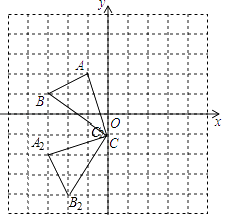
（3）
解：△A2B2C2的面积=3×3﹣ 
×1×3﹣ ×2×1﹣ ×3×2= 
．
【解析】（1）根据关于原点对称点的性质得出A，B，C对应点，进而得出答案；（2）根据平面直角坐标系写出点A2的坐标即可．（3）利用面积的和差求解：把三角形ABC的面积看作一个正方形的面积减去三个直角三角形的面积．
【考点精析】解答此题的关键在于理解关于原点对称的点的坐标的相关知识，掌握两个点关于原点对称时，它们的坐标的符号相反，即点P（x，y）关于原点的对称点为P’（-x，-y）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两同学的家与学校的距离均为3000米．甲同学先步行600米，然后乘公交车去学校、乙同学骑自行车去学校．已知甲步行速度是乙骑自行车速度的
，公交车的速度是乙骑自行车速度的2倍．甲乙两同学同时从家发去学校，结果甲同学比乙同学早到2分钟．（1）求乙骑自行车的速度；
（2）当甲到达学校时，乙同学离学校还有多远？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，AD∥BC，E是AB的中点，连接DE并延长交CB的延长线于点F，点G在边BC上，且∠GDF=∠ADF．
（1）求证：△ADE≌△BFE；
（2）连接EG，判断EG与DF的位置关系并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1：在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°．E、F分别是BC、CD上的点．且∠EAF＝60°．探究图中线段BE、EF、FD之间的数量关系．
小王同学探究此问题的方法是，延长FD到点G，使DG＝BE．连结AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是 ；
探索延伸：
如图2，若在四边形ABCD中，AB＝AD，∠B＋∠D＝180°．E、F分别是BC、CD上的点，且∠EAF＝
∠BAD，上述结论是否仍然成立，并说明理由；实际应用：
如图3，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西30°的A处，舰艇乙在指挥中心南偏东70°的B处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以60海里/小时的速度前进，舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇之间的夹角为70°，试求此时两舰艇之间的距离？
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，△ABC中，BO，CO分别是∠ABC和∠ACB的平分线，过O点的直线分别交AB、AC于点D、E，且DE∥BC．若AB=6 cm，AC=8 cm，则△ADE的周长为__________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，如图，AB是⊙O的直径，C为⊙O上一点，AD垂直于经过点C的直线DE，垂足为点D，AC平分∠DAB．
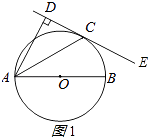
（1）求证：直线DE是⊙O的切线；
（2）连接BC，猜想：∠ECB与∠CAB的数量关系，并证明你的猜想． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，D是等边三角形ABC内一点，将线段AD绕点A顺时针旋转60°，得到线段AE，连接CD，BE．
（1）求证：∠AEB=∠ADC；
（2）连接DE，若∠ADC=105°，求∠BED的度数．
相关试题
