【题目】如图,在8×8的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1;(要求:A与A1,B与B1,C与C1相对应)
(2)![]() 是 三角形;
是 三角形;
(3)若有一格点P到点A、B的距离相等(PA=PB),则网格中满足条件的点P共有 个;
(4)在直线![]() 上找一点Q,使QB+QC的值最小。
上找一点Q,使QB+QC的值最小。

参考答案:
【答案】(1)答案见解析;(2)等腰直角;(3)4;(4)答案见解析.
【解析】
(1)分别作出点A、B、C关于直线l的对称点,再顺次连接可得;
(2)根据网格,求出AB,AC,BC的长度,然后再判断即可;
(3)作线段AB的垂直平分线,即可得到答案;
(4)连接![]() ,与
,与![]() 相交于一点,这点为点Q,由垂直平分线性质,QC=
相交于一点,这点为点Q,由垂直平分线性质,QC=![]() ,则得到QB+QC的最小值.
,则得到QB+QC的最小值.
解:(1)如图所示:△A1B1C1为所求.
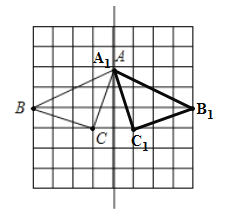
(2)根据题意,可知,
![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 是等腰直角三角形;
是等腰直角三角形;
故答案为:等腰直角.
(3)如图,作线段AB的垂直平分线,与网格的顶点相交即为点P;

由图可知,使PA=PB的点P一共有4个,
故答案为:4.
(4)如图,连接![]() 与
与![]() 相交于点Q,则QB+QC取到最小值;
相交于点Q,则QB+QC取到最小值;
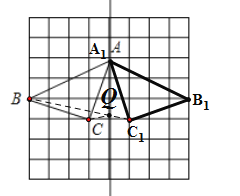
∵![]() 垂直平分
垂直平分![]() ,
,
∴![]() ,
,
∴QB+QC=QB+![]() ,
,
∴最小值为:![]() ;
;
-
科目: 来源: 题型:
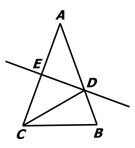
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AC的垂直平分线分别交AB、AC于点D、E.
(1)若∠A = 40°,求∠DCB的度数.
(2)若AE=4,△DCB的周长为14,求△ABC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知在
 中,BE平分
中,BE平分 交AC于点E,
交AC于点E, 交AB于点D,
交AB于点D, ,则
,则 的度数为________.
的度数为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为300,测得大楼顶端 A的仰角为450(点B,C,E在同一水平直线上)。已知AB=50m,DE=10m,求障碍物B,C两点间的距离。(结果精确到1m,参考数据:
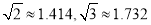 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平面直角坐标系中,一次函数
 的图象与反比例函数
的图象与反比例函数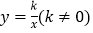 的图象交于一、三象限内的A、B两点,与x轴交于C点,点A的坐标为
的图象交于一、三象限内的A、B两点,与x轴交于C点,点A的坐标为 ,点B的坐标为
,点B的坐标为 ,
, .
. 求该反比例函数和一次函数的解析式;
求该反比例函数和一次函数的解析式; 在x轴上有一点
在x轴上有一点 点除外
点除外 ,使得
,使得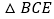 与
与 的面积相等,求出点E的坐标.
的面积相等,求出点E的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点A1(1,1),第二次向右跳动3个单位至点A2(2,1),第三次跳动至点A3(2,2),第四次向右跳动5个单位至点A4(3,2),…,以此规律跳动下去,点A第100次跳动至点A100的坐标是()

A.(50,50)B.(51,51)C.(51,50)D.(50,51)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, ,点B在x轴上,且
,点B在x轴上,且 .
. 求点B的坐标;
求点B的坐标; 求
求 的面积;
的面积; 在y轴上是否存在P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请求出点P的坐标;若不存在,请说明理由.
在y轴上是否存在P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请求出点P的坐标;若不存在,请说明理由.
相关试题

