【题目】已知四边形ABCD是正方形,△ADE是等边三角形,求∠BEC的度数.
参考答案:
【答案】 30°或者150°.
【解析】试题分析:分当等边△ADE在正方形ABCD外部时(如图①)和当等边△ADE在正方形ABCD内部时(如图②)两种情况求解.
试题解析:
(1)当等边三角形ADE在正方形ABCD外部时,如图①所示.
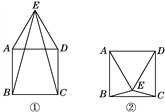
∵AB=AD=AE,∠BAE=90°+60°=150°,
∴∠AEB=(180°-150°)÷2=15°.
同理,∠DEC=15°.∴∠BEC=60°-15°-15°=30°.
(2)当等边三角形ADE在正方形ABCD内部时,如图②所示.
∵AB=AD=AE,∠BAE=90°-60°=30°,
∴∠AEB=(180°-30°)÷2=75°.
同理,∠DEC=75°.∴∠BEC=360°-75°×2-60°=150°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. a+a=a2 B. 3x﹣2x=1
C. 5x2y﹣7x2y=2x2y D. 3ab﹣4ab=﹣ab
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=3是关于x的一元一次方程ax﹣6=0的解,则a的值为( )
A. ﹣2 B. 2 C. 3 D. ﹣3
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x一元二次方程x2+mx+n=0.
(1)当m=n+2时,利用根的判别式判断方程根的情况.
(2)若方程有实数根,写出一组满足条件的m,n的值,并求此时方程的根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:
(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;
(3)如图3,在(2)的基础上,连接AE和EF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法不正确的是( )
A.0既不是正数,也不是负数
B.1是绝对值最小的正数
C.一个有理数不是整数就是分数
D.0的绝对值是0 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,最适合采用全面调查(普查)方式的是( )
A. 对国庆期间来渝游客满意度的调查
B. 对我校某班学生数学作业量的调查
C. 对全国中学生手机使用时间情况的调查
D. 环保部门对嘉陵江水质情况的调查
相关试题

