【题目】解下列方程
(1)x2+x﹣1=0
(2)x(x﹣2)+x﹣2=0.
参考答案:
【答案】
(1)
解:△=12﹣4×1×(﹣1)=5,
x= ![]() ,
,
所以x1= ![]() ,x2=
,x2= ![]()
(2)
解:(x﹣2)(x+1)=0,
x﹣2=0或x+1=0,
所以x1=2,x2=﹣1
【解析】(1)利用公式法解方程;(2)利用因式分解法解方程.
【考点精析】解答此题的关键在于理解公式法的相关知识,掌握要用公式解方程,首先化成一般式.调整系数随其后,使其成为最简比.确定参数abc,计算方程判别式.判别式值与零比,有无实根便得知.有实根可套公式,没有实根要告之,以及对因式分解法的理解,了解已知未知先分离,因式分解是其次.调整系数等互反,和差积套恒等式.完全平方等常数,间接配方显优势.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,设ON的反向延长线为OD,则∠COD= °,∠AOD= °.
(2)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,求∠AOM﹣∠NOC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,AB=2,点C在⊙O上,∠CAB=30°,D为
 的中点,P是直径AB上一动点,则PC+PD的最小值为 .
的中点,P是直径AB上一动点,则PC+PD的最小值为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=4cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<12),连接DE,当△BDE是直角三角形时,t的值为

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若将△ABC绕点C逆时针旋转90°后得到△A′B′C′,

(1)在图中画出△A′B′C′;
(2)求出点A经过的路径长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D、E分别在BC、AB上,且∠BDE=∠CAD.求证:△ADE∽△ABD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=x﹣1与反比例函数y=
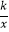 的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(﹣1,m).
的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(﹣1,m). 
(1)求反比例函数的解析式;
(2)若点P(n,﹣1)是反比例函数图象上一点,过点P作PE⊥x轴于点E,延长EP交直线AB于点F,求△CEF的面积.
相关试题

