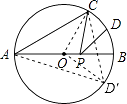
【题目】如图，AB是⊙O的直径，AB=2，点C在⊙O上，∠CAB=30°，D为 的中点，P是直径AB上一动点，则PC+PD的最小值为 ．

参考答案：

【答案】
【解析】解：作出D关于AB的对称点D′，连接OC，OD′，CD′． 又∵点C在⊙O上，∠CAB=30°，D为 的中点，即 = ，
∴∠BAD′= ∠CAB=15°．
∴∠CAD′=45°．
∴∠COD′=90°．则△COD′是等腰直角三角形．
∵OC=OD′= AB=1，
∴CD′= ．
所以答案是： ．

【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2，以及对垂径定理的理解，了解垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．

关闭