【题目】甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图所示.根据图象所提供的信息,下列说法正确的是( )
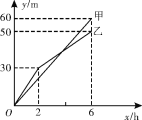
A. 甲队开挖到30 m时,用了2 h
B. 开挖6 h时,甲队比乙队多挖了60 m
C. 乙队在0≤x≤6的时段,y与x之间的关系式为y=5x+20
D. 当x为4 h时,甲、乙两队所挖河渠的长度相等
参考答案:
【答案】D
【解析】
选项A,观察图象即可解答;选项B,观察图象可知开挖6h时甲队比乙队多挖:60-50=10(m),由此即可判定选项B;选项C,根据图象,可知乙队挖河渠的长度y(m)与挖掘时间x(h)之间的函数关系是分段函数,由此即可判定选项C;选项D,分别求得施工4小时时甲、乙两队所挖河渠的长度,比较即可解答.
选项A,根据图示知,乙队开挖到30m时,用了2h,甲队开挖到30m时,用的时间是大于2h.故本选项错误;
选项B,由图示知,开挖6h时甲队比乙队多挖:60-50=10(m),即开挖6 h时甲队比乙队多挖了10m.故本选项错误;
选项C,根据图示知,乙队挖河渠的长度y(m)与挖掘时间x(h)之间的函数关系是分段函数:在0~2h时,y与x之间的关系式y=15x;在2~6h时,y与x之间的关系式y=5x+20.故本选项错误;
选项D,甲队4h完成的工作量是:(60÷6)×4=40(m),
乙队4h完成的工作量是:5×4+20=40(m),
∵40=40,
∴当x=4时,甲、乙两队所挖管道长度相同.故本选项正确;
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )
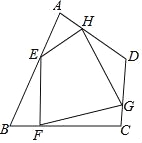
A.当E,F,G,H是各边中点,且AC=BD时,四边形EFGH为菱形
B.当E,F,G,H是各边中点,且AC⊥BD时,四边形EFGH为矩形
C.当E,F,G,H不是各边中点时,四边形EFGH可以为平行四边形
D.当E,F,G,H不是各边中点时,四边形EFGH不可能为菱形
-
科目: 来源: 题型:
查看答案和解析>>【题目】某次篮球联赛共有十支队伍参赛,部分积分表如下.根据表格提供的信息解答下列问题:
队名
比赛场次
胜场
负场
积分
A
18
14
4
32
B
18
11
7
29
C
18
9
9
27
(1)列一元一次方程求出胜一场、负一场各积多少分?
(2)某队的胜场总积分能等于它的负场总积分吗?若能,试求胜场数和负场数;若不能,说出理由.
(3)试就某队的胜场数求出该队的负场总积分是它的胜场总积分的正整数倍的情况?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC=2
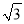 ,∠DAO=30°,则FC的长度为( )
,∠DAO=30°,则FC的长度为( ) 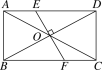
A. 1B. 2
C.
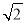 D.
D. 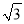
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一垂直于地面的灯柱AB被一钢筋CD固定,CD与地面成45°夹角(∠CDB=45°),在C点上方2米处加固另一条钢线ED,ED与地面成53°夹角(∠EDB=53°),那么钢线ED的长度约为多少米?(结果精确到1米,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
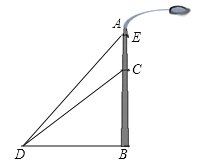
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知□ABCD的对角线AC、BD交于O,且∠1=∠2.
(1)求证:□ABCD是菱形;
(2)F为AD上一点,连结BF交AC于E,且AE=AF.求证:AO=
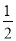 (AF+AB).
(AF+AB).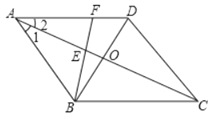
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校决定对学生感兴趣的球类项目(A:足球,B:篮球,C:排球,D:羽毛球,E:乒乓球)进行问卷调查,学生可根据自己的喜好选修一门,李老师对某班全班同学的选课情况进行统计后,制成了两幅不完整的统计图(如图).

(1)该班学生人数有 人;
(2)将条形统计图补充完整;
(3)若该校共有学生3500名,请估计有多少人选修足球?
(4)该班班委5人中,1人选修篮球,3人选修足球,1人选修排球,李老师要从这5人中任选2人了解他们对体育选修课的看法,请你用列表或画树状图的方法,求选出的2人恰好1人选修篮球,1人选修足球的概率.
相关试题

