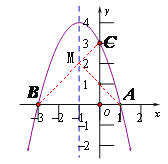
【题目】如图抛物线![]() 与
与![]() 轴交于A(1,0),
轴交于A(1,0),![]() 两点
两点

(1)求该抛物线的解析式;
(2)设(1)中的抛物线交![]() 轴于
轴于![]() 点,在该抛物线的对称轴上是否存在点
点,在该抛物线的对称轴上是否存在点![]() ,使得
,使得![]() 的周长最小?若存在,求出
的周长最小?若存在,求出![]() 点的坐标;若不存在,请说明理由。
点的坐标;若不存在,请说明理由。
参考答案:
【答案】(1)y=-x2-2x+3.(2)存在,(-1,2).
【解析】
试题分析:(1)将点A、点B的坐标代入可求出b、c的值,继而可得出该抛物线的解析式;
(2)连接BC,则BC与对称轴的交点,即是点M的位置,求出直线BC的解析式后,可得出点M的坐标.
试题解析:(1)把A(1,0)、B(-3,0)代入抛物线解析式可得:
![]() ,
,
解得:![]()
故抛物线的解析式为y=-x2-2x+3.
(2)存在.
由题意得,点B与点A关于抛物线的对称轴对称,连接BC,则BC与抛物线对称轴的交点是点M的位置,
设直线BC解析式为y=kx+b,把B(-3,0)、C(0,3)代入得:
![]() ,
,
解得:![]() ,
,
则直线BC的解析式为y=x+3,
令MX=-1得My=2,
故点M的坐标为:(-1,2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】李明到离家2.1千米的学校参加初三联欢会,到学校时发现演出道具还放在家中,此时距联欢会开始还有42分钟,于是他立即匀速步行回家,在家拿道具用了1分钟,然后立即匀速骑自行车返回学校.已知李明骑自行车到学校比他从学校步行到家用时少20分钟,且骑自行车的速度是步行速度的3倍.
(1)李明步行的速度(单位:米/分)是多少?
(2)李明能否在联欢会开始前赶到学校?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:(单位:米)+5,-3,+10,-8,-6,+12,-10
(1)守门员最后是否回到了球门线的位置?
(2)在练习过程中,守门员离开球门最远距离是多少米?
(3)守门员全部练习结束后,他共跑了多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)当销售单价为70元时,每天的销售利润是多少?
(2)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式,并求出自变量
 的取值范围;
的取值范围;(3)如果该企业每天的总成本不超过7000元,那么销售单价为多少元时,每天的销售利润最大?最大利润是多少?(每天的总成本=每件的成本×每天的销售量)
-
科目: 来源: 题型:
查看答案和解析>>【题目】大润发超市进了一批成本为8元/个的文具盒。调查发现: 这种文具盒每个星期的销售量
 个)与它的定价
个)与它的定价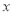 (元/个)的关系如图所示:
(元/个)的关系如图所示: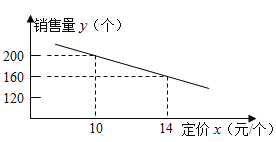
(1)求这种文具盒每个星期的销售量
 个)与它的定价
个)与它的定价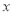 (元/个)之间的函数关系式(不必写出自变量
(元/个)之间的函数关系式(不必写出自变量 的取值范围)
的取值范围)(2)每个文具盒定价是多少元时,超市每星期销售这种文具盒(不考虑其他因素)可获得的利润最高?最高利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(小时)之间的关系如图所示,请根据图象所提供的信息解答下列问题:
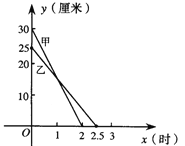
(1)甲、乙两根蜡烛燃烧前的高度分别是 ,从点燃到燃尽甲所用的时间为 .
(2)分别求甲、乙两根蜡烛燃烧时y与x之间的函数关系式;
(3)燃烧多长时间时,甲、乙两根蜡烛的高度相等(不考虑都燃尽时的情况)?在什么时间段内,甲蜡烛比乙蜡烛高?在什么时间段内,甲蜡烛比乙蜡低?
-
科目: 来源: 题型:
查看答案和解析>>【题目】 “十
 一”黄金周期间,西安大唐芙蓉园在7天假期中每天接待游客的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)。
一”黄金周期间,西安大唐芙蓉园在7天假期中每天接待游客的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)。日期
10月1日
10月2日
10月3日
10月4日
10月5日
10月6日
10月7日
人数变化
(万人)
+1.6
+0.8
+0.4
-0.4
-0.8
+0.2
-1.4
(1)若9月30日的游客人数为
 万人,则10月2日的游客人数为_______万人;
万人,则10月2日的游客人数为_______万人;(2)七天内游客人数最大的是10月_______日;
(3)若9月30日游客人数为3万人,门票每人120元。请求出黄金周期间西安大唐芙蓉园门票总收入是多少万元?
相关试题

