【题目】如图矩形ABCD中,AD=1,CD= ![]() ,连接AC,将线段AC、AB分别绕点A顺时针旋转90°至AE、AF,线段AE与弧BF交于点G,连接CG,则图中阴影部分面积为 .
,连接AC,将线段AC、AB分别绕点A顺时针旋转90°至AE、AF,线段AE与弧BF交于点G,连接CG,则图中阴影部分面积为 . 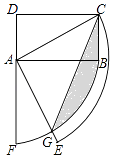
参考答案:
【答案】![]() ﹣
﹣ ![]()
【解析】解:在矩形ABCD中,
∵AD=1,CD= ![]() ,
,
∵AC=2,tan∠CAB= ![]() =
= ![]() ,
,
∴∠CAB=30°,
∵线段AC、AB分别绕点A顺时针旋转90°至AE、AF,
∴∠CAE=∠BAF=90°,
∴∠BAG=60°,
∵AG=AB= ![]() ,
,
∴阴影部分面积=S△ABC+S扇形ABG﹣S△ACG= ![]() ×
× ![]() ×1+
×1+ ![]() ﹣
﹣ ![]() ×
× ![]() ×2=
×2= ![]() ﹣
﹣ ![]() ,
,
所以答案是: ![]() ﹣
﹣ ![]() .
.
【考点精析】解答此题的关键在于理解矩形的性质的相关知识,掌握矩形的四个角都是直角,矩形的对角线相等,以及对扇形面积计算公式的理解,了解在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1,先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2017次,点B的落点依次为B1 , B2 , B3 , …,则B2017的坐标为( )
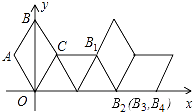
A.(1345,0)
B.(1345.5,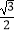 )
)
C.(1345,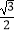 )
)
D.(1345.5,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正整数能表示成两个连续偶数的平方差,那么这个正整数为“神秘数”.
如:


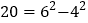
因此,4,12,20这三个数都是神秘数.
(1)28和2012这两个数是不是神秘数?为什么?
(2)设两个连续偶数为
 和
和 (其中
(其中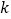 为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由. (3)两个连续奇数的平方差(取正数)是不是神秘数?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 长方形的长是
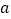 米,宽比长短25米,则它的周长可表示为
米,宽比长短25米,则它的周长可表示为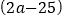 米
米B.
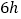 表示底为6,高为
表示底为6,高为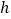 的三角形的面积
的三角形的面积C.
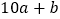 表示一个两位数,它的个位数字是
表示一个两位数,它的个位数字是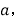 十位数字是
十位数字是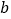
D. 甲、乙两人分别从相距40千米的两地相向出发,其行走的速度分别为3千米/小时和5千米/小时,经过
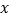 小时相遇,则可列方程为
小时相遇,则可列方程为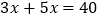
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有2019条直线
 且有
且有 …,则直线
…,则直线 与
与 的位置关系是___________.
的位置关系是___________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC∥BD,要使△ABC≌△BAD需再补充一个条件,下列条件中,不能选择的是( )
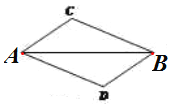
A. BC∥AD B. AC=BD C. BC=AD D. ∠C=∠D
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)(x+y)2-2x(x+y); (2)(a+1)(a-1)-(a-1)2;
(3)先化简,再求值:
(x+2y)(x-2y)-(2x3y-4x2y2)÷2xy,其中x=-3,
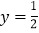 .
.
相关试题

