【题目】如图,在Rt△ACB中,∠ACB=90°,∠A=30°,点D是AB边的中点.
(1)如图1,若CD=4,求△ACB的周长.
(2)如图2,若E为AC的中点,将线段CE以C为旋转中心顺时针旋转60°,使点E至点F处,连接BF交CD于点M,连接DF,取DF的中点N,连接MN,求证:MN=2CM.
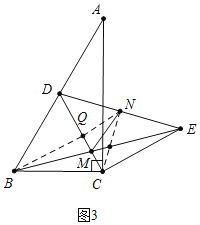
(3)如图3,以C为旋转中心将线段CD顺时针旋转90°,使点D至点E处,连接BE交CD于M,连接DE,取DE的中点N,连接交MN,试猜想BD、MN、MC之间的关系,直接写出其关系式,不证明.

参考答案:
【答案】(1)12+4![]() ;(2)证明见解析;(3)证明见解析.
;(2)证明见解析;(3)证明见解析.
【解析】(1)根据直角三角形斜边中线的性质,直角三角形30度角性质以及勾股定理即可解决问题.
(2)如图2中,作BQ⊥CD于Q,FP∥MN交DC的延长线于P.首先证明△BQM≌△FCM,推出QC=2CM,再证明△BQC≌△FCP,推出PF=BC=2QC,再根据三角形中位线定理即可解决问题.
(3)结论:(![]() BD)2+(
BD)2+(![]() BD-CM)2=MN2.作BQ⊥CD于Q,连接QN,只要证明△QMN是直角三角形,QN=
BD-CM)2=MN2.作BQ⊥CD于Q,连接QN,只要证明△QMN是直角三角形,QN=![]() BD,QM=
BD,QM=![]() BD-CM即可解决问题.
BD-CM即可解决问题.
如图1中,
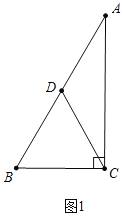
在Rt△ACB中,∵∠ACB=90°,∠A=30°,点D是AB边的中点.
∴CD=BD=AD=4,BC=![]() AB=4,
AB=4,
∴AC=![]() =
=![]() ,
,
∴△ABC的周长为4+8+4![]() =12+4
=12+4![]() .
.
(2)证明:如图2中,作BQ⊥CD于Q,FP∥MN交DC的延长线于P.
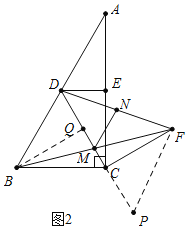
∵△BDC是等边三角形,边长为2,
∴高BQ=2![]() ,∠DCB=60°,∠ACD=30°
,∠DCB=60°,∠ACD=30°
∵EA=EC=2![]() ,
,
∴CE=CF=BQ,
∵∠ECF=60°,∠ACD=30°,
∴∠DCF=90°,
∴∠BQM=∠MCF=90°,
在△BQM和△FCM中,
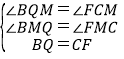 ,
,
∴△BQM≌△FCM,
∴QM=MC.QC=2MC,
∵DN=NF,MN∥FP,
∴DM=MP,
∴DQ=CP=QC,
在△BQC和△FCP中,
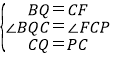 ,
,
∴△BQC≌△FCP,
∴PF=BC=DC=2QC,
∵MN=![]() PF,
PF,
∴MN=QC=2CM.
(3)解:如图3中,结论:(![]() BD)2+(
BD)2+(![]() BD-CM)2=MN2.理由如下:
BD-CM)2=MN2.理由如下:
作BQ⊥CD于Q,连接QN,
∵△BDC是等边三角形,
∴∠DBQ=30°,
∴DQ=QC=![]() BD,
BD,
∵DC=CE,DC⊥CE,
∴∠CDE=∠CED=45°,
∵DQ=QC,DN=NE,
∴QN∥EC,
∴∠QDN=∠NQM=∠DCE=90°,
∴∠QDN=∠QND=45°,
∴QD=QN=![]() BD,
BD,
∵QN2+QM2=MN2,
∴(![]() BD)2+(
BD)2+(![]() BD-CM)2=MN2.
BD-CM)2=MN2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
①(x﹣3)﹣3(3x﹣1)=1
②老师在黑板上出了一道解方程的题
 =1﹣
=1﹣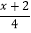 ,小明马上举手,要求到黑板上做,他是这样做的:
,小明马上举手,要求到黑板上做,他是这样做的:4(2x﹣1)=1﹣3(x+2)…①
8x﹣4=1﹣3x﹣6…②
8x+3x=1﹣6+4…③
11x=﹣1…④
x=﹣
 …⑤
…⑤老师说:小明解一元一次方程的一般步骤都知道却没有掌握好,因此解题时有一步出现了错误,请你指出他错在那一步(填编号),并写出正确的解答过程.
 =1﹣
=1﹣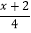
③当m为何值时,关于x的方程5m+3x=1+x的解比关于x的方程2x+m=3m的解小2?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点C,D在线段AB上,M、N分别是AC、BD的中点,若AB=20,CD=4,
(1)求MN的长.
(2)若AB=a,CD=b,请用含有a、b的代数式表示出MN的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在圣诞节来临之际,某儿童商场用2800元购进了一批玩具,上市后很快售完,商场又用7200元购进第二批这种玩具,所购数量是第一批购进数量的2倍,但每个玩具进价多了4元.
(1)该商场两次共购进这批玩具多少个?
(2)如果这两批玩具每个的售价相同,且全部售完后总利润率不低于20%,那么每个玩具的售价至少是多少元?
-
科目: 来源: 题型:
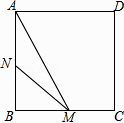
查看答案和解析>>【题目】如图,正方形ABCD的边长为3cm,动点M从点B出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达点A停止运动,另一动点N同时从点B出发,以1cm/s的速度沿着边BA向点A运动,到达点A停止运动,设点M运动时间为x(s),△AMN的面积为y(cm2),则y关于x的函数图象是( )
A.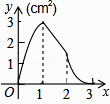
B.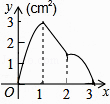
C.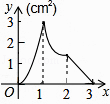
D.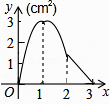
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.

(1)射线OC的方向是___________________;
(2)求∠COD的度数;
(3)若射线OE平分∠COD,求∠AOE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B分别为数轴上的两点,A点对应的数为﹣20,B点对应的数为100.

(1)请写出与A,B两点距离相等的点M所对应的数 .
(2)现有一只电子蚂蚁P从B点出发,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度向右运动,x秒后两只电子蚂蚁在数轴上的C点相遇,请列方程求出x,并指出点C表示的数.
(3)若当电子蚂蚁P从B点出发时,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度也向左运动,y秒后两只电子蚂蚁在数轴上的D点相遇,请列方程求出y并指出点D表示的数.
相关试题

