【题目】【探索发现】
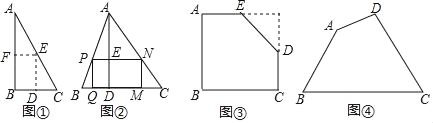
如图①,是一张直角三角形纸片,∠B=90°,小明想从中剪出一个以∠B为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE、EF剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为 .
【拓展应用】
如图②,在△ABC中,BC=a,BC边上的高AD=h,矩形PQMN的顶点P、N分别在边AB、AC上,顶点Q、M在边BC上,则矩形PQMN面积的最大值为 .(用含a,h的代数式表示)
【灵活应用】
如图③,有一块“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角),求该矩形的面积.
【实际应用】
如图④,现有一块四边形的木板余料ABCD,经测量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC=![]() ,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.
,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.
参考答案:
【答案】详见解析.
【解析】试题解分析:【探索发现】:由中位线知EF=![]() BC、ED=
BC、ED=![]() AB、由
AB、由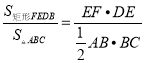 可得;
可得;
【拓展应用】:由△APN∽△ABC知![]() ,可得PN=a-
,可得PN=a-![]() PQ,设PQ=x,由S矩形PQMN=PQPN═-
PQ,设PQ=x,由S矩形PQMN=PQPN═-![]() (x-
(x-![]() )2+
)2+![]() ,据此可得;
,据此可得;
【灵活应用】:添加如图1辅助线,取BF中点I,FG的中点K,由矩形性质知AE=EH=20、CD=DH=16,分别证△AEF≌△HED、△CDG≌△HDE得AF=DH=16、CG=HE=20,从而判断出中位线IK的两端点在线段AB和DE上,利用【探索发现】结论解答即可;
【实际应用】:延长BA、CD交于点E,过点E作EH⊥BC于点H,由tanB=tanC知EB=EC、BH=CH=54,EH=![]() BH=72,继而求得BE=CE=90,可判断中位线PQ的两端点在线段AB、CD上,利用【拓展应用】结论解答可得.
BH=72,继而求得BE=CE=90,可判断中位线PQ的两端点在线段AB、CD上,利用【拓展应用】结论解答可得.
试题解析:【探索发现】
∵EF、ED为△ABC中位线,
∴ED∥AB,EF∥BC,EF=![]() BC,ED=
BC,ED=![]() AB,
AB,
又∠B=90°,
∴四边形FEDB是矩形,
则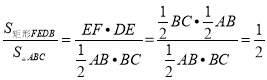 ;
;
【拓展应用】
∵PN∥BC,
∴△APN∽△ABC,
∴![]() ,即
,即![]() ,
,
∴PN=a-![]() PQ,
PQ,
设PQ=x,
则S矩形PQMN=PQPN=x(a-![]() x)=-
x)=-![]() x2+ax=-
x2+ax=-![]() (x-
(x-![]() )2+
)2+![]() ,
,
∴当PQ=![]() 时,S矩形PQMN最大值为
时,S矩形PQMN最大值为![]() .
.
【灵活应用】
如图1,延长BA、DE交于点F,延长BC、ED交于点G,延长AE、CD交于点H,取BF中点I,FG的中点K,
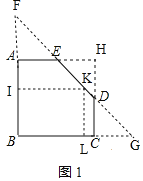
由题意知四边形ABCH是矩形,
∵AB=32,BC=40,AE=20,CD=16,
∴EH=20、DH=16,
∴AE=EH、CD=DH,
在△AEF和△HED中,
∵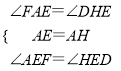 ,
,
∴△AEF≌△HED(ASA),
∴AF=DH=16,
同理△CDG≌△HDE,
∴CG=HE=20,
∴BI=![]() =24,
=24,
∵BI=24<32,
∴中位线IK的两端点在线段AB和DE上,
过点K作KL⊥BC于点L,
由【探索发现】知矩形的最大面积为![]() ×BG
×BG![]() BF=
BF=![]() ×(40+20)×
×(40+20)×![]() (32+16)=720,
(32+16)=720,
答:该矩形的面积为720;
【实际应用】
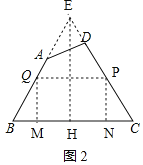
如图2,延长BA、CD交于点E,过点E作EH⊥BC于点H,
∵tanB=tanC=![]() ,
,
∴∠B=∠C,
∴EB=EC,
∵BC=108cm,且EH⊥BC,
∴BH=CH=![]() BC=54cm,
BC=54cm,
∵tanB=![]() =
=![]() ,
,
∴EH=![]() BH=
BH=![]() ×54=72cm,
×54=72cm,
在Rt△BHE中,BE=![]() =90cm,
=90cm,
∵AB=50cm,
∴AE=40cm,
∴BE的中点Q在线段AB上,
∵CD=60cm,
∴ED=30cm,
∴CE的中点P在线段CD上,
∴中位线PQ的两端点在线段
由【拓展应用】知,矩形PQMN的最大面积为![]() BCEH=1944cm2,
BCEH=1944cm2,
答:该矩形的面积为1944cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
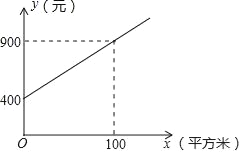
甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)的关系如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,超过的部分每月每平方米加收4元.
(1)求如图所示的y与x的函数表达式;
(2)如果某学校目前的绿化面积是1200平方米.那么选择哪家公司的服务比较划算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列生活、生产现象中,可以用基本事实“两点确定一条直线”来解释的有( )
①用两颗钉子就可以把木条固定在墙上
②把笔尖看成一个点,当这个点运动时便得到一条线;
③把弯曲的公路改直,就能缩短路程;
④植树时,只要栽下两棵树,就可以把同一行树栽在同一条直线上。
A.
 个B.
个B. 个C.
个C. 个D.
个D. 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数
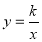 的图象经过点A(﹣1,a),过点A作AB⊥x轴,垂足为点B,△AOB的面积为
的图象经过点A(﹣1,a),过点A作AB⊥x轴,垂足为点B,△AOB的面积为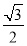 .
.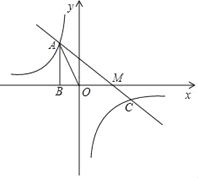
(1)求k的值;
(2)若一次函数y=mx+n图象经过点A和反比例函数图象上另一点
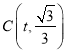 ,且与x轴交于M点,求AM的值;
,且与x轴交于M点,求AM的值;(3)在(2)的条件下,如果以线段AM为一边作等边△AMN,顶点N在另一个反比例函数
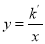 上,则k'= .
上,则k'= . -
科目: 来源: 题型:
查看答案和解析>>【题目】某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价40元。厂方在开展促销活动期间,向客户提供两种优惠方案:
①买一套西装送一条领带;②西装和领带都按定价的90%付款。现某客户要到该服装厂购买西装20套,领带x条(
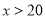 ):
):(1)若该客户按方案①购买,需付款______________元(用含x的代数式表示);若该客户按方案②购买,需付款________________元(用含x的代数式表示);
(2)若x=30,通过计算说明此时按哪种方案购买较为合算?
(3)当x=30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知矩形OABC的顶点B(6,8),动点M,N同时从O点出发,点M沿射线OA方向以每秒1个单位的速度运动,点N沿线段OB方向以每秒0.6个单位的速度运动,当点N到达点B时,点M,N同时停止运动,连接MN,设运动时间为t(秒).
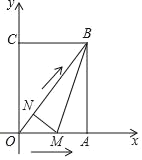
(1)求证△ONM~△OAB;
(2)当点M是运动到点
 时,若双曲线
时,若双曲线 的图象恰好过点N,试求k的值;
的图象恰好过点N,试求k的值;(3)△MNB与△OAB能否相似?若能试求出所有t的值,若不能请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示4和1的两点之间的距离是 ;表示﹣3和2两点之间的距离是 ;一般地,数轴上表示数m和数n的两点之间的距离等于|m﹣n|.如果表示数a和﹣2的两点之间的距离是3,那么a= ;
(2)若数轴上表示数a的点位于﹣4与2之间,求|a+4|+|a﹣2|的值;
(3)当a取何值时,|a+5|+|a﹣1|+|a﹣4|的值最小,最小值是多少?请说明理由.
相关试题

