【题目】如图,已知点![]() 分别在线段
分别在线段![]() 上,
上,![]() 交
交![]() 于点
于点![]() 平分
平分![]() .
.
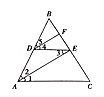
(1)求证:![]() 平分
平分![]() 阅读下列推理过程,并将推理过程补充完整.
阅读下列推理过程,并将推理过程补充完整.
证明:![]() 平分
平分![]() ,(已知)
,(已知)
![]() (角平分线的定义)
(角平分线的定义)
![]() ,(已知)
,(已知)
![]() ( )
( )
故 .(等量代换)
![]() ,(已知)
,(已知)
![]() ,( )
,( )
![]() ,( )
,( )
![]() ,
,
![]() 平分
平分![]() .( )
.( )
(2)若![]() ,请直接写出图中所有与
,请直接写出图中所有与![]() 互余的角.
互余的角.
参考答案:
【答案】(1)![]() ;两直线平行,内错角相等;
;两直线平行,内错角相等;![]() ;两直线平行,同位角相等;两直线平行,内错角相等;角平分线的定义;(2)
;两直线平行,同位角相等;两直线平行,内错角相等;角平分线的定义;(2)![]() 和
和![]()
【解析】
(1)根据角平分线的定义得到∠1=∠2,根据平行线的性质得到∠1=∠3,等量代换得到∠2=∠3,根据平行线的性质得到∠2=∠5,等量代换即可得到结论;
(2)根据垂直的定义得到∠3+∠DEB=90°,∠1+∠C=90°,由平行线的性质得出∠5+∠B=90°,然后由∠3=∠1=∠4=∠5得出与∠1互余的角.
解:(1)![]() 平分
平分![]() ,(已知)
,(已知)
![]() (角平分线的定义)
(角平分线的定义)
![]() ,(已知)
,(已知)
![]() ,(两直线平行,内错角相等)
,(两直线平行,内错角相等)
故![]() (等量代换)
(等量代换)
![]() ,(已知)
,(已知)
![]() ,(两直线平行,同位角相等)
,(两直线平行,同位角相等)
![]() ,(两直线平行,内错角相等)
,(两直线平行,内错角相等)
![]() ,(等量代换)
,(等量代换)
![]() 平分
平分![]() .(角平分线的定义)
.(角平分线的定义)
故答案为:![]() ;两直线平行,内错角相等;
;两直线平行,内错角相等;![]() ;两直线平行,同位角相等;两直线平行,内错角相等;角平分线的定义;
;两直线平行,同位角相等;两直线平行,内错角相等;角平分线的定义;
(2)∵![]() ,
,![]()
∴∠AEB=∠DFB=90°
∴∠3+∠DEB=90°,∠1+∠C=90°,∠5+∠B=90°,
又由①可知∠3=∠1=∠4=∠5
∴∠1+∠DEB=90°,∠1+∠B=90°,
∴与![]() 互余的角有
互余的角有![]() 和
和![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△AEF中,∠EAF=45°,AG⊥EF于点G,现将△AEG沿AE折叠得到△AEB,将△AFG沿AF折叠得到△AFD,延长BE和DF相交于点C.
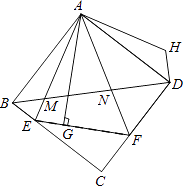
(1)求证:四边形ABCD是正方形;
(2)连接BD分别交AE、AF于点M、N,将△ABM绕点A逆时针旋转,使AB与AD重合,得到△ADH,试判断线段MN、ND、DH之间的数量关系,并说明理由.
(3)若EG=4,GF=6,BM=3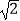 ,求AG、MN的长.
,求AG、MN的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小强从A处出发沿北偏东70°方向行走,走至B处,又沿着北偏西30°方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是( )
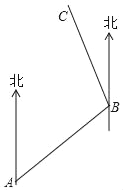
A. 左转 80° B. 右转80° C. 右转 100° D. 左转 100°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD=AE,添加下列条件仍无法证明△ABE≌△ACD的是( )
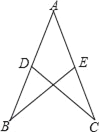
A. AB=AC B. ∠B=∠C
C. BE=CD D. ∠ADC=∠AEB
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场服装部为了调动营业员的积极性,决定实行目标管理,即确定一个月销售目标,根据目标完成的情况对营业员进行适当的奖惩.为了确定一个适当的目标,商场统计了每个营业员在某月的销售额,统计图如下:
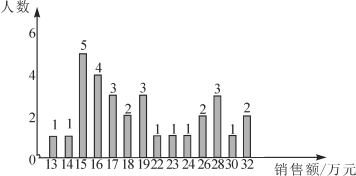
请你结合统计图和平均数、众数和中位数解答下列问题:(结果保留整数)
(1)月销售额在哪个值的人最多?月销售额处于中间的是多少?月平均销售额是多少?
(2)如果想确定一个较高的销售目标,你认为月销售额定为多少合适?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半圆O的直径AB=4,P,Q是半圆O上的点,弦PQ的长为2,则
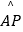 与
与  的长度之和为( )
的长度之和为( ) 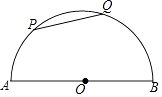
A.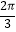
B.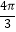
C.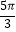
D.π -
科目: 来源: 题型:
查看答案和解析>>【题目】木工师傅要做一个如图所示的窗框,上半部分是半圆,下半部分为六个大小一样的长方形,长方形的长和宽的比为
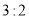 .请你帮他计算:
.请你帮他计算: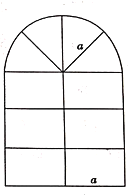
(1)设长方形的长为
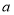 米,用含
米,用含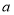 的代数式表示所需材料的长度为 (结果保留
的代数式表示所需材料的长度为 (结果保留 ,重合部分忽略不计)
,重合部分忽略不计)(2)当长方形的长为
 米时,所需材料的长度是多少?(精确到
米时,所需材料的长度是多少?(精确到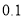 米,其中
米,其中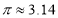 )
)
相关试题

