【题目】如图,在平面直角坐标系中, A(0,2),B(-1,0),Rt△AOC的面积为4.
(1)求点C的坐标;
(2)抛物线![]() 经过A、B、C三点,求抛物线的解析式和对称轴;
经过A、B、C三点,求抛物线的解析式和对称轴;
(3)设点P(m,n)是抛物线在第一象限部分上的点,△PAC的面积为S,求S关于m的函数关系式,并求使S最大时点P的坐标.

参考答案:
【答案】(1)C(4,0);(2)![]() ,对称轴
,对称轴 ![]() ;(3)
;(3)![]() ,P(2,3).
,P(2,3).
【解析】分析:(1)由A(0,2),可得OA=2,再由Rt△AOC的面积为4,得OC的值,即可求了C点的坐标,(2)设抛物线的解析式为:y=ax2+bx+c,把A(0,2),B(-1,0),C(4,0)代入,即可求出抛物线的解析式,可得出对称轴,(3)由点A,C的坐标,可求出直线AC的解析式,过点P作PQ⊥x轴于H,交直线AC于Q,过点P作PM⊥AC于点M,由OA=2,OC=4,可得AC的值,从而得出cos∠ACO的值,设P(m,n),Q(m,-![]() m+2),可求出PQ,利用
m+2),可求出PQ,利用![]() ,解得PM,由n= -
,解得PM,由n= -![]() m+
m+![]() m+2,得PM=
m+2,得PM=![]() ×(-
×(-![]() m+2m),再由三角形的面积公式即可求出S=-2m+8m,即可得出当m=2,即P(2,3)时,S的值最大.
m+2m),再由三角形的面积公式即可求出S=-2m+8m,即可得出当m=2,即P(2,3)时,S的值最大.
本题解析:
(1)C(4,0)
(2)抛物线的解析式:![]() ,对称轴
,对称轴 ![]() .
.
(3)设直线AC的解析式为:![]() ,代入点A(0,2),C(4,0),得:
,代入点A(0,2),C(4,0),得:
∴直线AC:![]() ;
;
过点P作PQ⊥x轴于H,交直线AC于Q,
设P(![]() ,
,![]() ),Q(
),Q(![]() ,
,![]() )
)
则![]()
∴![]()
∴当m=2,即 P(2,3)时,S的值最大.

点睛: 本题主要考查了二次次函数与方程、几何知识的综合应用,解题的关键是善于将函数问题转化为方程问题,善于利用几何图形的关性质、定理和二次函数的知识求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=120
 ,BC=6cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为( )
,BC=6cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为( )
A. 1.5cm B. 2cm C. 2.5cm D. 3cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A.平面内过一点有且只有一条直线与已知直线垂直
B.两点之间的所有连线中,线段最短
C.经过两点有且只有一条直线
D.经过一点有且只有一条直线
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x2﹣4=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:ax+ay= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,点M、N分别在AB、BC上,将BMN沿MN翻折,得FMN,若MF∥AD,FN∥DC,则∠D的度数为_________
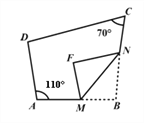
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校小组5名同学的身高(单位:cm)分别为:147,151,152,156,159,则这组数据的中位数是( )
A.147
B.151
C.152
D.156
相关试题

