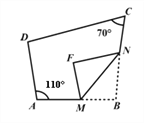
【题目】如图,四边形ABCD中,点M、N分别在AB、BC上,将BMN沿MN翻折,得FMN,若MF∥AD,FN∥DC,则∠D的度数为_________
参考答案:
【答案】90
【解析】首先利用平行线的性质得出∠BNF=100°,∠FNB=70°,再利用翻折变换的性质得出∠FMN=∠BMN=50°,∠FNM=∠MNB=35°,进而求出∠B的度数以及得出∠D度数.
解:∵MF∥AD,FN∥DC,∠A=100°,∠C=70°,
∴∠BMF=100°,∠FNB=70°,
∵将△BMN沿MN翻折,得△FMN,
∴∠FMN=∠BMN=50°,∠FNM=∠MNB=35°,
∴∠F=∠B=180°-50°-35°=95°
∴∠D=360°-100°-70°-90°=95°.
“点睛”此题主要考查了平行线的性质以及多边形内角和定理以及翻折变换的性质,得出∠FMN=∠BMN,∠FNM=∠MNB是解题关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x2﹣4=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中, A(0,2),B(-1,0),Rt△AOC的面积为4.
(1)求点C的坐标;
(2)抛物线
 经过A、B、C三点,求抛物线的解析式和对称轴;
经过A、B、C三点,求抛物线的解析式和对称轴;(3)设点P(m,n)是抛物线在第一象限部分上的点,△PAC的面积为S,求S关于m的函数关系式,并求使S最大时点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:ax+ay= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校小组5名同学的身高(单位:cm)分别为:147,151,152,156,159,则这组数据的中位数是( )
A.147
B.151
C.152
D.156 -
科目: 来源: 题型:
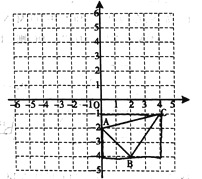
查看答案和解析>>【题目】已知:如图,△ABC.
(1)分别画出与△ABC关于x轴、y轴对称的图形△A1B1C1和△A2B2C2;
(2)写出△A1B1C1和△A2B2C2各顶点的坐标;
(3)直接写出△ABC的面积,
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠α与∠β互余,且∠α=35°,则∠β的补角为_________.
相关试题

