搜索
【题目】如图，四边形ABCD为圆内接四边形，AB是直径，MN切⊙O于C点，∠BCM=38°，那么∠ABC的度数是（ ） 
A.38°
B.52°
C.68°
D.42°
参考答案：
【答案】B
【解析】解：连接OC，如图，
∵MN切⊙O于C点，
∴OC⊥MN，
∴∠OCM=90°，
∴∠OCB=90°﹣∠BCM=90°﹣38°=52°，
而OB=OC，
∴∠ABC=∠OCB=52°．
故选B．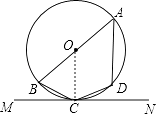
【考点精析】根据题目的已知条件，利用圆内接四边形的性质和切线的性质定理的相关知识可以得到问题的答案，需要掌握把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线，以相邻切线的交点为顶点的多边形是这个圆的外切正n边形；切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径．
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲仓库有水泥100吨，乙仓库有水泥80吨，要全部运动A、B两工地，已知A工地需要70吨，B工地需要110吨，甲仓库运到A、B两工地的运费分别是140元/吨、150元/吨，乙仓库运到A、B两工地的运费分别是200元/吨、80元/吨，本次运送水泥总运费需要25900元，问甲仓库运到A工地水泥的吨数．（运费：元/吨，表示运送每吨水泥所需的人民币）
（1）设甲仓库运到A工地水泥的吨数为x吨，请在下面表格中用x表示出其他未知量．
甲仓库
乙仓库
A工地
x
B工地
x+10
（2）用含x的代数式表示运送甲仓库100吨水泥的运费为 元．（写出化简后的结果）
（3）请根据题目中的等量关系和以上的分析列出方程．（只列出方程即可，写成ax+b=0的形式，不用解）
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，
是边长为3cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速移动，它们的速度都是
，当点P到达点B时，P、Q两点停止运动，设点P的运动时间
，解答下列各问题：
经过
秒时，求
的面积；
当t为何值时， 
是直角三角形？
是否存在某一时刻t，使四边形APQC的面积是
面积的三分之二？如果存在，求出t的值；不存在请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=x2﹣3x+
与x轴相交于A、B两点，与y轴相交于点C，点D是直线BC下方抛物线上一点，过点D作y轴的平行线，与直线BC相交于点E 
（1）求A、B的坐标；
（2）求直线BC的解析式；
（3）当线段DE的长度最大时，求点D的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米，先到终点的人原地休息．已知甲先出发2秒，在跑步过程中，甲、乙两人间的距离y(米)与乙出发的时间t(秒)之间的关系如图所示，给出以下结论：①a＝8；②c＝92；③b＝123.其中正确的是( )
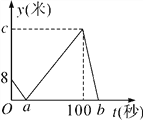
A. ①②
B. ②③
C. ①③
D. ①②③
-
科目： 来源： 题型：
查看答案和解析>>【题目】把一副三角板如图甲放置，其中∠ACB=∠DEC=90°，∠A=45°，∠D=30°，斜边AB=12，DC=14，把三角板DCE绕点C顺时针旋转15°得到△D1CE1（如图乙），此时AB与 CD1交于点O，则线段AD1的长为（ ）
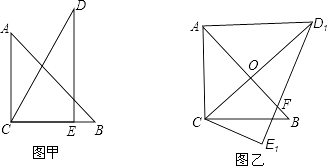
A.6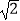
B.10
C.8
D.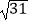
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将直线y＝－x沿y轴向下平移后的直线恰好经过点A(2，－4)，且与y轴交于点B，在x轴上存在一点P使得PA＋PB的值最小，则点P的坐标为________．
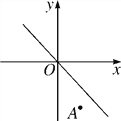
相关试题
