【题目】如图,∠AOB=90°,∠BOC=30°,射线OM平分∠AOC,ON平分∠BOC. 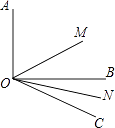
(1)求∠MON的度数;
(2)如果(1)中,∠AOB=α,其他条件不变,求∠MON的度数;
(3)如果(1)中,∠BOC=β(β为锐角),其他条件不变,求∠MON的度数;
(4)从(1)、(2)、(3)的结果中,你能看出什么规律?
参考答案:
【答案】
(1)解:∠AOB=90°,∠BOC=30°,
∴∠AOC=90°+30=120°.
由角平分线的性质可知:∠MOC= ![]() ∠AOC=60°,∠CON=
∠AOC=60°,∠CON= ![]() ∠BOC=15°.
∠BOC=15°.
∵∠MON=∠MOC﹣∠CON,
∴∠MON=60°﹣15°=45°
(2)解:∠AOB=α,∠BOC=30°,
∴∠AOC=α+30°.
由角平分线的性质可知:∠MOC= ![]() ∠AOC=
∠AOC= ![]() α+15°,∠CON=
α+15°,∠CON= ![]() ∠BOC=15°.
∠BOC=15°.
∵∠MON=∠MOC﹣∠CON,
∴∠MON= ![]() α+15°﹣15°=
α+15°﹣15°= ![]() α
α
(3)解:∠AOB=90°,∠BOC=β,
∴∠AOC=β+90°.
由角平分线的性质可知:∠MOC= ![]() ∠AOC=
∠AOC= ![]() β+45°,∠CON=
β+45°,∠CON= ![]() ∠BOC=
∠BOC= ![]() β.
β.
∵∠MON=∠MOC﹣∠CON,
∴∠MON= ![]() β+45°﹣
β+45°﹣ ![]() β=45°
β=45°
(4)解:根据(1)、(2)、(3)可知∠MON= ![]() ∠BOC,与∠BOC的大小无关
∠BOC,与∠BOC的大小无关
【解析】(1)先求得∠AOC的度数,然后由角平分线的定义可知∠MOC=60°,∠CON=15°,最后根据∠MON=∠MOC﹣∠CON求解即可;(2)先求得∠AOC=α+30°,由角平分线的定义可知∠MOC= ![]() α+15°,∠CON=15°,最后根据∠MON=∠MOC﹣∠CON求解即可;(3)先求得∠AOC=β+90°,由角平分线的定义可知∠MOC=
α+15°,∠CON=15°,最后根据∠MON=∠MOC﹣∠CON求解即可;(3)先求得∠AOC=β+90°,由角平分线的定义可知∠MOC= ![]() β+15°,∠CON=
β+15°,∠CON= ![]() β,最后根据∠MON=∠MOC﹣∠CON求解即可;(4)根据计算结果找出其中的规律即可.
β,最后根据∠MON=∠MOC﹣∠CON求解即可;(4)根据计算结果找出其中的规律即可.
【考点精析】认真审题,首先需要了解角的平分线(从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线),还要掌握角的运算(角之间可以进行加减运算;一个角可以用其他角的和或差来表示)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求证:角的平分线上的点到角的两边的距离相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿边AB向点B以2cm/s的速度移动,点Q从点B开始沿边BC向点C以4cm/s的速度移动,如果点P、Q分别从点A、B同时出发,经几秒钟△PBQ与△ABC相似?试说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某地方政府决定在相距50km的A、B两站之间的公路旁E点,修建一个土特产加工基地,且使C、D两村到E点的距离相等,已知DA⊥AB于A,CB⊥AB于B,DA=30km,CB=20km,那么基地E应建在离A站多少千米的地方?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上,点A所表示的数为4,那么到点A的距离等于5个单位长度的点所表示的数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. a+a=a2B. 6a3﹣5a2=a
C. (2x5)2=4x10D. a6÷a2=a3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
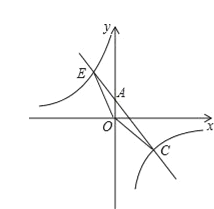
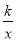 的图象与一次函数y=ax﹢b的图象交于C(4,﹣3),E(﹣3,4)两点.且一次函数图象交y轴于点A.
的图象与一次函数y=ax﹢b的图象交于C(4,﹣3),E(﹣3,4)两点.且一次函数图象交y轴于点A.(1)求反比例函数与一次函数的解析式;
(2)求△COE的面积;
(3)点M在x轴上移动,是否存在点M使△OCM为等腰三角形?若存在,请你直接写出M点的坐标;若不存在,请说明理由.
相关试题

