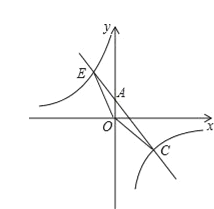
【题目】如图,反比例函数y=![]() 的图象与一次函数y=ax﹢b的图象交于C(4,﹣3),E(﹣3,4)两点.且一次函数图象交y轴于点A.
的图象与一次函数y=ax﹢b的图象交于C(4,﹣3),E(﹣3,4)两点.且一次函数图象交y轴于点A.
(1)求反比例函数与一次函数的解析式;
(2)求△COE的面积;
(3)点M在x轴上移动,是否存在点M使△OCM为等腰三角形?若存在,请你直接写出M点的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)一次函数的解析式为y=﹣x+1.
(2)S△COE=S△AOE+S△AOC=![]() ×1×3+
×1×3+![]() ×1×4=3.5.
×1×4=3.5.
(3)点M坐标为M1(8,0)或M2(5,0)或M3(﹣5,0)或M4(![]() ,0).
,0).
【解析】
试题分析:(1)点C(4,﹣3)坐标代入反比例函数y=![]() 即可求出k,C(4,﹣3),E(﹣3,4)两点坐标代入y=ax+b解方程组即可求出a、b.由此即可解决问题.
即可求出k,C(4,﹣3),E(﹣3,4)两点坐标代入y=ax+b解方程组即可求出a、b.由此即可解决问题.
(2)先求出点A坐标,根据S△COE=S△AOE+S△AOC计算即可.
(3)分三种情形①当CM=OC时,可得M1(8,0).②当OC=OM时,可得M2(5,0),M3(﹣5,0).②当MC=MO时,设M4(x,0),则有x2=(x﹣4)2+32,解方程即可.
试题解析:(1)∵反比例函数y=![]() 的图象经过点C(4,﹣3),
的图象经过点C(4,﹣3),
∴﹣3=![]() ,∴k=﹣12,∴反比例函数解析式为y=﹣
,∴k=﹣12,∴反比例函数解析式为y=﹣![]() ,
,
∵y=ax+b的图象经过C(4,﹣3),E(﹣3,4)两点,
∴![]() ,解得
,解得![]() ,∴一次函数的解析式为y=﹣x+1.
,∴一次函数的解析式为y=﹣x+1.
(2)∵一次函数的解析式为y=﹣x+1与y轴交于点A(0,1),∴S△COE=S△AOE+S△AOC=![]() ×1×3+
×1×3+![]() ×1×4=3.5.
×1×4=3.5.
(3)如图,∵C(4,﹣3),∴OC=![]() =5,
=5,

①当CM=OC时,可得M1(8,0).②当OC=OM时,可得M2(5,0),M3(﹣5,0).
②当MC=MO时,设M4(x,0),则有x2=(x﹣4)2+32,解得x=![]() ,∴M4(
,∴M4(![]() ,0).
,0).
综上所述,点M坐标为M1(8,0)或M2(5,0)或M3(﹣5,0)或M4(![]() ,0).
,0).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=90°,∠BOC=30°,射线OM平分∠AOC,ON平分∠BOC.
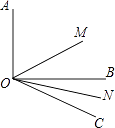
(1)求∠MON的度数;
(2)如果(1)中,∠AOB=α,其他条件不变,求∠MON的度数;
(3)如果(1)中,∠BOC=β(β为锐角),其他条件不变,求∠MON的度数;
(4)从(1)、(2)、(3)的结果中,你能看出什么规律? -
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上,点A所表示的数为4,那么到点A的距离等于5个单位长度的点所表示的数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. a+a=a2B. 6a3﹣5a2=a
C. (2x5)2=4x10D. a6÷a2=a3
-
科目: 来源: 题型:
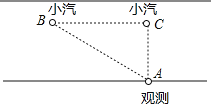
查看答案和解析>>【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70千米/小时,如图,一辆小汽车在一条城市街道上直道行驶,某一时刻刚好行驶到路面对车速检测仪正前方30米C处,过了2秒后,小汽车行驶到B处,测得小汽车与车速检测仪间距离为50米,
(1)求BC的长;
(2)这辆小汽车超速了吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加快4G网络建设,某市电信运营企业根据自身发展规划,2014年计划完成投资28000000元,将28000000用科学记数法可表示为( )
A. 2.8×104B. 0.28×108C. 2.8×107D. 28×105
-
科目: 来源: 题型:
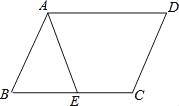
查看答案和解析>>【题目】在平行四边形ABCD中,E为BC边上的一点.连结AE.
(1)若AB=AE,求证:∠DAE=∠D;
(2)若点E为BC的中点,连接BD,交AE于F,求EF:FA的值.
相关试题

