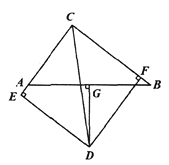
【题目】如图,△ABC中,AC=6,BC=8,AB=10,∠BCA的平分线与AB的垂直平分线DG交于点D,DE⊥CA的延长线于点E,DF⊥CB于点F.
(1)判断△ABC的形状,并说明理由;
(2)求证:AE=BF;
(3)求DG的长.
参考答案:
【答案】(1)直角三角形;(2)过程见解析;(3)5.
【解析】
(1)根据勾股定理的逆定理即可判断△ABC是直角三角形;
(2)根据中垂线、角平分线的性质来证明Rt△AED≌Rt△BFD,然后根据全等三角形的对应边相等推知AE=BF;
(3)首先根据(1)和(2)得出的结论,证明△ADB是直角三角形,再利用三线合一的性质和直角三角形斜边上的中线等于斜边的一半,进而得出DG.
解:(1)∵AC=6,BC=8,AB=10,
∴AC2+BC2=AB2,
∴△ABC是直角三角形;
(2)证明:连接AD、BD,
∵CD是∠BCA的平分线,DE⊥AC,DF⊥BC,
∴DE=DF,
∵DG是AB边的垂直平分线,
∴DA=DB,
在Rt△AED和Rt△BFD中,
![]()
∴Rt△AED≌Rt△BFD(HL),
∴AE=BF;
(3)由(1)得∠ACB=90°,
∵∠E=∠DFC=90°
∴∠EDF=90°,
由(2)知∠EDA=∠FDB,
∴∠ADB=90°,
∵DG⊥AB,DA=DB,
∴DG=![]() AB=5.
AB=5.
故答案为:(1)直角三角形;(2)过程见解析;(3)5.
-
科目: 来源: 题型:
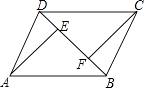
查看答案和解析>>【题目】如图,在四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E,F,求证:四边形AFCE是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热[此过程中水温y(℃)与开机时间x(分)满足一次函数关系],当加热到100℃时自动停止加热,随后水温开始下降[此过程中水温y(℃)与开机时间x(分)成反比例关系],当水温降至20℃时,饮水机又自动开始加热…,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:

(1)当0≤x≤8时,求水温y(℃)与开机时间x(分)的函数关系式;
(2)求图中t的值;
(3)若小明在通电开机后即外出散步,请你预测小明散步45分钟回到家时,饮水机内的温度约为多少℃? -
科目: 来源: 题型:
查看答案和解析>>【题目】一个等腰三角形的周长为25cm.
(1)已知腰长是底边长的2倍,求各边的长;
(2)已知其中一边的长为6cm.求其它两边的长.
-
科目: 来源: 题型:
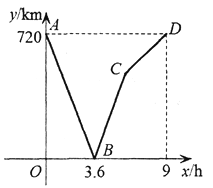
查看答案和解析>>【题目】一辆快车与一辆慢车分别从甲、乙两地同时出发,沿同一路线相向 而行,抵达对方出发地时停止运动.设慢车行驶xh时,两车之间的路程为ykm.图中折线ABCD表示y与x的函数关系,根据图像,解决以下问题:
(1)慢车的速度为多少km/h,快车的速度为多少km/h;
(2)解释图中点C的实际意义,求出点C的坐标;
(3)当x取何值时,y=500 ?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资量x成正比例关系,种植花卉的利润y2与投资量x的平方成正比例关系,并得到了表格中的数据.
投资量x(万元)
2
种植树木利润y1(万元)
4
种植花卉利润y2(万元)
2
(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,设他投入种植花卉金额m万元,种植花卉和树木共获利利润W万元,直接写出W关于m的函数关系式,并求他至少获得多少利润?他能获取的最大利润是多少?
(3)若该专业户想获利不低于22万,在(2)的条件下,直接写出投资种植花卉的金额m的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】吉林省广播电视塔(简称“吉塔”)是我省目前最高的人工建筑,也是俯瞰长春市美景的最佳去处.某科技兴趣小组利用无人机搭载测量仪器测量“吉塔”的高度.已知如图将无人机置于距离“吉塔”水平距离138米的点C处,则从无人机上观测塔尖的仰角恰为30°,观测塔基座中心点的俯角恰为45°.求“吉塔”的高度.(注:
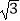 ≈1.73,结果保留整数)
≈1.73,结果保留整数)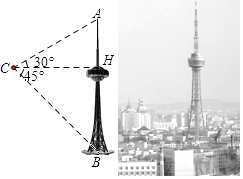
相关试题

