【题目】某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资量x成正比例关系,种植花卉的利润y2与投资量x的平方成正比例关系,并得到了表格中的数据.
投资量x(万元) | 2 |
种植树木利润y1(万元) | 4 |
种植花卉利润y2(万元) | 2 |
(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,设他投入种植花卉金额m万元,种植花卉和树木共获利利润W万元,直接写出W关于m的函数关系式,并求他至少获得多少利润?他能获取的最大利润是多少?
(3)若该专业户想获利不低于22万,在(2)的条件下,直接写出投资种植花卉的金额m的范围.
参考答案:
【答案】
(1)解:设y1=kx,
由表格数据可知,函数y1=kx的图象过(2,4),
∴4=k2,
解得:k=2,
故利润y1关于投资量x的函数关系式是y1=2x(x≥0);
∵设y2=ax2,
由表格数据可知,函数y2=ax2的图象过(2,2),
∴2=a22,
解得:a= ![]() ,
,
故利润y2关于投资量x的函数关系式是:y2= ![]() x2(x≥0);
x2(x≥0);
(2)解:因为种植花卉m万元(0≤m≤8),则投入种植树木(8﹣m)万元,
w=2(8﹣m)+ ![]() m2=
m2= ![]() m2﹣2m+16=
m2﹣2m+16= ![]() (m﹣2)2+14,
(m﹣2)2+14,
∵a=0.5>0,0≤m≤8,
∴当m=2时,w的最小值是14,
∵a= ![]() >0,
>0,
∴当m>2时,w随m的增大而增大
∵0≤m≤8,
∴当m=8时,w的最大值是32,
答:他至少获得14万元利润,他能获取的最大利润是32万元.
(3)解:根据题意,当w=22时, ![]() (m﹣2)2+14=22,
(m﹣2)2+14=22,
解得:m=﹣2(舍)或m=6,
故:6≤m≤8.
【解析】(1)根据题意设y1=kx、y2=ax2,将表格中数据分别代入求解可得;(2)由种植花卉m万元(0≤m≤8),则投入种植树木(8﹣m)万元,根据“总利润=花卉利润+树木利润”列出函数解析式,利用二次函数的性质求得最值即可;(3)根据获利不低于22万,列出不等式求解可得.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个等腰三角形的周长为25cm.
(1)已知腰长是底边长的2倍,求各边的长;
(2)已知其中一边的长为6cm.求其它两边的长.
-
科目: 来源: 题型:
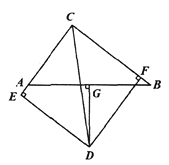
查看答案和解析>>【题目】如图,△ABC中,AC=6,BC=8,AB=10,∠BCA的平分线与AB的垂直平分线DG交于点D,DE⊥CA的延长线于点E,DF⊥CB于点F.
(1)判断△ABC的形状,并说明理由;
(2)求证:AE=BF;
(3)求DG的长.
-
科目: 来源: 题型:
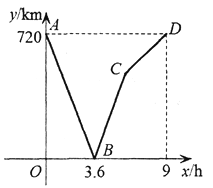
查看答案和解析>>【题目】一辆快车与一辆慢车分别从甲、乙两地同时出发,沿同一路线相向 而行,抵达对方出发地时停止运动.设慢车行驶xh时,两车之间的路程为ykm.图中折线ABCD表示y与x的函数关系,根据图像,解决以下问题:
(1)慢车的速度为多少km/h,快车的速度为多少km/h;
(2)解释图中点C的实际意义,求出点C的坐标;
(3)当x取何值时,y=500 ?
-
科目: 来源: 题型:
查看答案和解析>>【题目】吉林省广播电视塔(简称“吉塔”)是我省目前最高的人工建筑,也是俯瞰长春市美景的最佳去处.某科技兴趣小组利用无人机搭载测量仪器测量“吉塔”的高度.已知如图将无人机置于距离“吉塔”水平距离138米的点C处,则从无人机上观测塔尖的仰角恰为30°,观测塔基座中心点的俯角恰为45°.求“吉塔”的高度.(注:
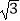 ≈1.73,结果保留整数)
≈1.73,结果保留整数)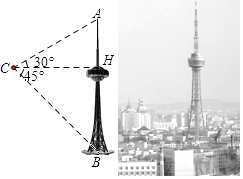
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学初三(1)班共有40名同学,在一次30秒跳绳测试中他们的成绩统计如下表:
跳绳数/个
81
85
90
93
95
98
100
人 数
1
2
8
11
5
将这些数据按组距5(个)分组,绘制成如图的频数分布直方图(不完整).
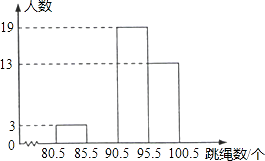
(1)将表中空缺的数据填写完整,并补全频数分布直方图;
(2)这个班同学这次跳绳成绩的众数是个,中位数是个;
(3)若跳满90个可得满分,学校初三年级共有720人,试估计该中学初三年级还有多少人跳绳不能得满分. -
科目: 来源: 题型:
查看答案和解析>>【题目】决心试一试,请阅读下列材料:计算:

解法一:原式=

=

=

解法二:原式=

=

=

=

解法三:原式的倒数为:

=

=﹣20+3﹣5+12
=﹣10
故原式 =

上述得出的结果不同,肯定有错误的解法,你认为解法 是错误的,在正确的解法中,你认为解法 最简捷.然后请解答下列问题,计算:
 .
.
相关试题

