【题目】(1)如图,因为直线AB、CD相交于点P,AB∥EF,所以CD不平行于EF(________________________________________________________);
(2)因为直线a∥b,b∥c,所以a∥c(________________________________).
![]()
参考答案:
【答案】经过直线外一点,有且只有一条直线与这条直线平行 平行于同一直线的两条直线平行
【解析】
(1)利用经过直线外一点,有且只有一条直线与这条直线平行,进而得出答案;
(2)利用平行于同一直线的两条直线平行进而得出答案.
(1)如图,因为直线AB、CD相交于点P,AB∥EF,所以CD不平于EF(经过直线外一点,有且只有一条直线与这条直线平行);
故答案为:经过直线外一点,有且只有一条直线与这条直线平行.
(2)因为直线a∥b,b∥c,所以a∥c(平行于同一直线的两条直线平行).
故答案为:平行于同一直线的两条直线平行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】截长补短法,是初中几何题中一种添加辅助线的方法,也是把几何题化难为易的一种策略.截长就是在长边上截取一条线段与某一短边相等,补短就是通过延长或旋转等方式使两条短边拼合到一起,从而解决问题.
(1)如图1,△ABC是等边三角形,点D是边BC下方一点,∠BDC=120°,探索线段DA、DB、DC之间的数量关系.
解题思路:延长DC到点E,使CE=BD,根据∠BAC+∠BDC=180°,可证∠ABD=∠ACE,易证△ABD≌△ACE,得出△ADE是等边三角形,所以AD=DE,从而解决问题.
根据上述解题思路,三条线段DA、DB、DC之间的等量关系是;(直接写出结果)
(2)如图2,Rt△ABC中,∠BAC=90°,AB=AC.点D是边BC下方一点,∠BDC=90°,探索三条线段DA、DB、DC之间的等量关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=x2﹣(k+1)x+k与x轴相交于A、B两点(点B位于点A的左侧),与y轴相交于点C.
(1)如图1,若k=2,直接写出AB的长:AB= .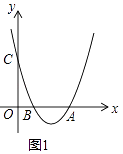
(2)若AB=2,则k的值为 .
(3)如图2,若k=﹣3,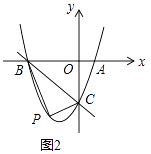
①求直线BC的解析式;
(4)如图3,若k<0,且△ABC是等腰三角形,求k的值.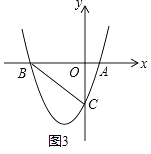
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E是AB上一动点(不与点A,B重合),点F在AD上,过点E作EG⊥EF交BC于点G,连接FG.

(1)当BE=AF时,求证:EF=EG
(2)若AB=4,AF=1,且设AE=n,
①当FG∥AB时,求n的值;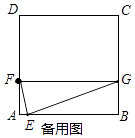
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索与发现:
(1)若直线a1⊥a2,a2∥a3,则直线a1与a3的位置关系是__________,请说明理由.
(2)若直线a1⊥a2,a2∥a3,a3⊥a4,则直线a1与a4的位置关系是________.(直接填结论,不需要证明)
(3)现在有2 011条直线a1,a2,a3,…,a2 011,且有a1⊥a2,a2∥a3,a3⊥a4,a4∥a5…,请你探索直线a1与a2 011的位置关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,AB=AC,∠C=70°,△AB′C′与△ABC 关于直线 EF对称,∠CAF=10°,连接 BB′,则∠ABB′的度数是( )

A. 30° B. 35° C. 40° D. 45°
相关试题

