【题目】如图,在正方形ABCD中,点E是AB上一动点(不与点A,B重合),点F在AD上,过点E作EG⊥EF交BC于点G,连接FG.
(1)当BE=AF时,求证:EF=EG
(2)若AB=4,AF=1,且设AE=n,
①当FG∥AB时,求n的值;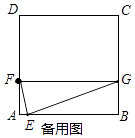
参考答案:
【答案】
(1)
∵四边形ABCD是正方形,
∴∠A=∠B=90°,
∵EG⊥EF,
∴∠AEF+∠BEG=90°,
∵∠AFE+∠AEF=90°,
∴∠AFE=∠BEG,
在△AEF和△BGE中,
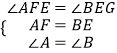 ,
,
∴△AEF≌△BGE(ASA),
∴EF=EG;
(2)
∵FG∥AB,
∴BG=AF=1,
∵AB=4,AE=n,
∴BE=4﹣n,
由(1)可得∠A=∠B=90°,∠AFE=∠BEG,
∴△AEF∽△BGE,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴解得n1=2﹣ ![]() ,n2=2+
,n2=2+ ![]() ;
;
②当BG取最大值时,求△EFG的面积.
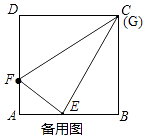
∵△AEF∽△BGE,
∴ ![]() =
= ![]() ,
,
∴BG= ![]() =n(4﹣n)=﹣n2+4n=﹣(n﹣2)2+4,
=n(4﹣n)=﹣n2+4n=﹣(n﹣2)2+4,
∴当n=2时,BG有最大值4,
此时点G与点C重合,
∴EF= ![]() =
= ![]() =
= ![]() ,
,
EG= ![]() =
= ![]() =2
=2 ![]() ,
,
∴△EFG的面积= ![]() EG×EF=
EG×EF= ![]() ×
× ![]() ×2
×2 ![]() =5.
=5.
【解析】(1)根据正方形的性质,判定△AEF≌△BGE,即可得出EF=EG;(2)①根据∠A=∠B=90°,∠AFE=∠BEG,即可判定△AEF∽△BGE,进而得到 ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,据此可得n的值;②根据△AEF∽△BGE,得出
,据此可得n的值;②根据△AEF∽△BGE,得出 ![]() =
= ![]() ,即BG=
,即BG= ![]() =n(4﹣n)=﹣n2+4n=﹣(n﹣2)2+4,进而得到当n=2时,BG有最大值4,据此可得点G与点C重合,再根据勾股定理求得EF=
=n(4﹣n)=﹣n2+4n=﹣(n﹣2)2+4,进而得到当n=2时,BG有最大值4,据此可得点G与点C重合,再根据勾股定理求得EF= ![]() =
= ![]() ,EG=
,EG= ![]() =2
=2 ![]() ,最后根据△EFG的面积=
,最后根据△EFG的面积= ![]() EG×EF进行计算即可.
EG×EF进行计算即可.
【考点精析】本题主要考查了全等三角形的性质和相似三角形的性质的相关知识点,需要掌握全等三角形的对应边相等; 全等三角形的对应角相等;对应角相等,对应边成比例的两个三角形叫做相似三角形才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】截长补短法,是初中几何题中一种添加辅助线的方法,也是把几何题化难为易的一种策略.截长就是在长边上截取一条线段与某一短边相等,补短就是通过延长或旋转等方式使两条短边拼合到一起,从而解决问题.
(1)如图1,△ABC是等边三角形,点D是边BC下方一点,∠BDC=120°,探索线段DA、DB、DC之间的数量关系.
解题思路:延长DC到点E,使CE=BD,根据∠BAC+∠BDC=180°,可证∠ABD=∠ACE,易证△ABD≌△ACE,得出△ADE是等边三角形,所以AD=DE,从而解决问题.
根据上述解题思路,三条线段DA、DB、DC之间的等量关系是;(直接写出结果)
(2)如图2,Rt△ABC中,∠BAC=90°,AB=AC.点D是边BC下方一点,∠BDC=90°,探索三条线段DA、DB、DC之间的等量关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=x2﹣(k+1)x+k与x轴相交于A、B两点(点B位于点A的左侧),与y轴相交于点C.
(1)如图1,若k=2,直接写出AB的长:AB= .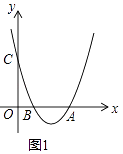
(2)若AB=2,则k的值为 .
(3)如图2,若k=﹣3,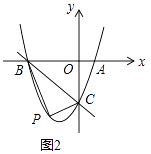
①求直线BC的解析式;
(4)如图3,若k<0,且△ABC是等腰三角形,求k的值.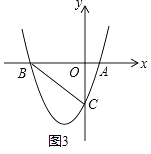
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,因为直线AB、CD相交于点P,AB∥EF,所以CD不平行于EF(________________________________________________________);
(2)因为直线a∥b,b∥c,所以a∥c(________________________________).
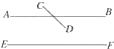
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索与发现:
(1)若直线a1⊥a2,a2∥a3,则直线a1与a3的位置关系是__________,请说明理由.
(2)若直线a1⊥a2,a2∥a3,a3⊥a4,则直线a1与a4的位置关系是________.(直接填结论,不需要证明)
(3)现在有2 011条直线a1,a2,a3,…,a2 011,且有a1⊥a2,a2∥a3,a3⊥a4,a4∥a5…,请你探索直线a1与a2 011的位置关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,AB=AC,∠C=70°,△AB′C′与△ABC 关于直线 EF对称,∠CAF=10°,连接 BB′,则∠ABB′的度数是( )

A. 30° B. 35° C. 40° D. 45°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=120
 ,BC=6cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为( )
,BC=6cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为( )
A. 1.5cm B. 2cm C. 2.5cm D. 3cm
相关试题

