搜索
【题目】如图．在Rt△ABC中，∠ABC=90°，点D是斜边上的中点，点P在AB上，PE⊥BD于E，PF⊥AC于F，若AB=6，BC=3，则PE+PF=（ ）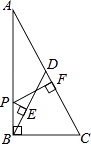 
A.
B.
C.
D.
参考答案：
【答案】A
【解析】解：如图作BM⊥AC于M，连接PD．
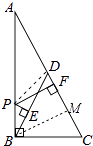
∵∠ABC=90°，AD=DC，AB=6，BC=3，
∴BD=AD=DC，AC= 
=3 
，
∵ 
ABBC= ACBM，
∴BM= 
，
∴S△ABD=S△ADP+S△BDP，
∴ ADBM= ADPF+ BDPE，
∴PE+PF=BM= ．
故选A．
【考点精析】解答此题的关键在于理解三角形的面积的相关知识，掌握三角形的面积=1/2×底×高，以及对直角三角形斜边上的中线的理解，了解直角三角形斜边上的中线等于斜边的一半．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列命题是真命题的是（ ）
A.一个角的补角一定大于这个角B.平行于同一条直线的两条直线平行
C.等边三角形是中心对称图形D.旋转改变图形的形状和大小
-
科目： 来源： 题型：
查看答案和解析>>【题目】类比、转化、从特殊到一般等思想方法，在数学学习和研究中经常用到，请看下面的案例．
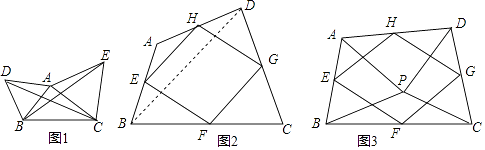
（1）如图1，已知△ABC，分别以AB、AC为边，在BC同侧作等边三角形ABD和等边三角形ACE，连接CD，BE．
通过证明△ ADC ≌△ ABE ，得到DC=BE；
（2）如图2，四边形ABCD中，点E，F，G，H分别为边AB，BC，CD，DA的中点，顺次连接E、F、G、H，得到四边形EFGH，我们称四边形EFGH为四边形ABCD的中点四边形，连接BD，利用三角形中位线的性质，可得EH∥BD，EH=
BD，同理可得FG∥BD，FG= BD，所以EH∥FG，EH=FG，所以四边形EFGH是平行四边形；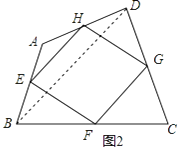
拓展应用
①如图3，点P是四边形ABCD内一点，且满足PA=PB，PC=PD，∠APB=∠CPD，点E，F，G，H分别为边AB，BC，CD，DA的中点，猜想四边形EFGH的形状，并证明；
（3）若改变（2）中的条件，使∠APB=∠CPD=90°，其他条件不变，四边形EFGH的形状是 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在下列三角形中，若AB＝AC ， 则能被一条直线分成两个小等腰三角形的是( )
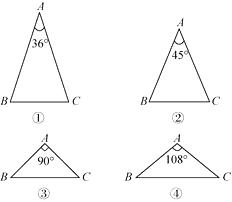
A.①②③
B.①②④
C.②③④
D.①③④ -
科目： 来源： 题型：
查看答案和解析>>【题目】-0.2的倒数是（ ）
A.-2B.-5C.5D.0.2
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示的一块地，已知∠ADC=90°，AD=12m，CD=9m，AB=25m，BC=20m，则这块地的面积为（ ）平方米．
A.96
B.204
C.196
D.304 -
科目： 来源： 题型：
查看答案和解析>>【题目】某种感冒病毒的直径是0.00000012米，将0.00000012用科学记数法可表示为 ．
相关试题
