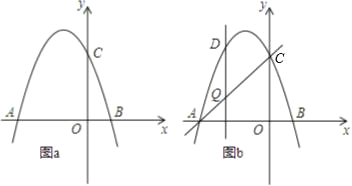
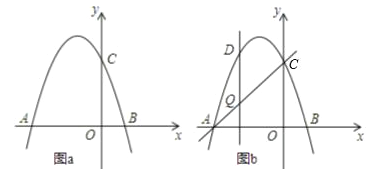
【题目】如图,抛物线y=-x2+bx+c交x轴于点A(-3,0)和点B,交y轴于点C(0,3).
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且S△AOP=4SBOC,求点P的坐标;
(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.
参考答案:
【答案】(1)抛物线的解析式为:y=-x2-2x+3.(2)点P的坐标为:(-1,4)或(-1+2![]() ,-4)或(-1-2
,-4)或(-1-2![]() ,-4);(3)QD有最大值
,-4);(3)QD有最大值![]() .
.
【解析】
试题分析:(1)把点A、C的坐标分别代入函数解析式,列出关于系数的方程组,通过解方程组求得系数的值;
(2)设P点坐标为(x,-x2-2x+3),根据S△AOP=4S△BOC列出关于x的方程,解方程求出x的值,进而得到点P的坐标;
(3)先运用待定系数法求出直线AC的解析式为y=x+3,再设Q点坐标为(x,x+3),则D点坐标为(x,x2+2x-3),然后用含x的代数式表示QD,根据二次函数的性质即可求出线段QD长度的最大值.
试题解析:(1)把A(-3,0),C(0,3)代入y=-x2+bx+c,得
![]() ,
,
解得![]() .
.
故该抛物线的解析式为:y=-x2-2x+3.
(2)由(1)知,该抛物线的解析式为y=-x2-2x+3,则易得B(1,0).
∵S△AOP=4S△BOC,
∴![]() ×3×|-x2-2x+3|=4×
×3×|-x2-2x+3|=4×![]() ×1×3.
×1×3.
整理,得(x+1)2=0或x2+2x-7=0,
解得x=-1或x=-1±2![]() .
.
则符合条件的点P的坐标为:(-1,4)或(-1+2![]() ,-4)或(-1-2
,-4)或(-1-2![]() ,-4);
,-4);
(3)设直线AC的解析式为y=kx+t,将A(-3,0),C(0,3)代入,
得![]() ,
,
解得![]() .
.
即直线AC的解析式为y=x+3.
设Q点坐标为(x,x+3),(-3≤x≤0),则D点坐标为(x,-x2-2x+3),
QD=(-x2-2x+3)-(x+3)=-x2-3x=-(x+![]() )2+
)2+![]() ,
,
∴当x=-![]() 时,QD有最大值
时,QD有最大值![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个数的平方根就是它本身,则这个数是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知实数m,n满足m﹣n2=1,则代数式m2+2n2+4m﹣1的最小值等于__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明坐于堤边垂钓,如图,河堤AC的坡角为30°,AC长
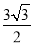 米,钓竿AO的倾斜角是60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.
米,钓竿AO的倾斜角是60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.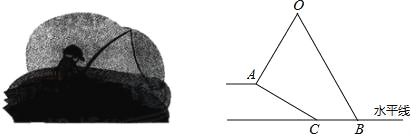
-
科目: 来源: 题型:
查看答案和解析>>【题目】若 x-3y=-5,则代数式 5-2x+6y 的值是( )
A. 0B. 5C. 10D. 15
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(20192-20182)0=_________________________ _.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知空气的单位体积质量是0.001239g/cm3,则用科学记数法表示该数为( )g/cm3.
A. 1.239×10﹣3 B. 1.2×10﹣3 C. 1.239×10﹣2 D. 1.239×10﹣4
相关试题

