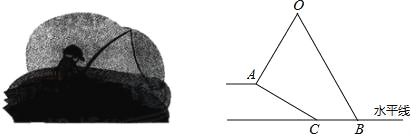
【题目】小明坐于堤边垂钓,如图,河堤AC的坡角为30°,AC长![]() 米,钓竿AO的倾斜角是60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.
米,钓竿AO的倾斜角是60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.
参考答案:
【答案】浮漂B与河堤下端C之间的距离为1.5米.
【解析】
试题分析:延长OA交BC于点D.先由倾斜角定义及三角形内角和定理求出∠CAD=180°-∠ODB-∠ACD=90°,解Rt△ACD,得出AD=ACtan∠ACD=![]() 米,CD=2AD=3米,
米,CD=2AD=3米,
再证明△BOD是等边三角形,得到BD=OD=OA+AD=4.5米,然后根据BC=BD-CD即可求出浮漂B与河堤下端C之间的距离.
试题解析:延长OA交BC于点D.
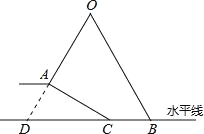
∵AO的倾斜角是60°,
∴∠ODB=60°.
∵∠ACD=30°,
∴∠CAD=180°-∠ODB-∠ACD=90°.
在Rt△ACD中,AD=ACtan∠ACD=![]() =
=![]() (米),
(米),
∴CD=2AD=3米,
又∵∠O=60°,
∴△BOD是等边三角形,
∴BD=OD=OA+AD=3+![]() =4.5(米),
=4.5(米),
∴BC=BD-CD=4.5-3=1.5(米).
答:浮漂B与河堤下端C之间的距离为1.5米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数y=x2﹣6x +m的图像与x轴只有一个公共点,则m=_______。
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个数的平方根就是它本身,则这个数是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知实数m,n满足m﹣n2=1,则代数式m2+2n2+4m﹣1的最小值等于__.
-
科目: 来源: 题型:
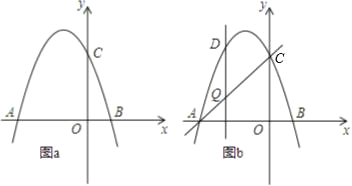
查看答案和解析>>【题目】如图,抛物线y=-x2+bx+c交x轴于点A(-3,0)和点B,交y轴于点C(0,3).
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且S△AOP=4SBOC,求点P的坐标;
(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若 x-3y=-5,则代数式 5-2x+6y 的值是( )
A. 0B. 5C. 10D. 15
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(20192-20182)0=_________________________ _.
相关试题

