搜索
【题目】下列命题中，真命题有（ ）
①直线外一点与直线上各点连接的所有线段中，垂线段最短；
②三角形的一个外角大于任何一个内角；
③如果∠1和∠2是对顶角，那么
；
④如果一条直线和两条直线中的一条垂直，那么这条直线也和另一条垂直．
A.1个B.2个C.3个D.4个
参考答案：
【答案】B
【解析】
本题主要利用垂线段性质，三角形角的大小，对顶角等知识点解题，重在对概念的理解与运用．
此题中①直线外一点与直线上各点连接的所有线段中，垂线段最短；此项正确；
②三角形的一个外角大于任何一个内角，比如钝角三角形就不满足；此项错误；
③如果∠1和∠2是对顶角，那么
；此项正确；
④如果一条直线和两条直线中的一条垂直，那么这条直线也和另一条垂直．前提条件是这两条直线平行，此项错误；
综上四条①③正确，故选B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，把矩形纸片ABCD沿EF折叠，使点B落在边AD上的点B′处，点A落在点A′处，已知AD=10，CD=4，B′D=2．
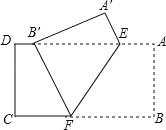
（1）求证：B′E=BF；
（2）求AE的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】四边形ABCD是正方形，E、F分别是DC和CB的延长线上的点，且DE=BF，连接AE、AF、EF．
（1）求证：△ADE≌△ABF；
（2）填空：△ABF可以由△ADE绕旋转中心 点，按顺时针方向旋转 度得到；
（3）若BC=8，DE=6，求△AEF的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，如图，O为坐标原点，四边形OABC为矩形，A（10，0），C（0，4），点D是OA的中点，点P在边BC上以每秒1个单位长的速度由点C向点B运动．
（1）当t为何值时，四边形PODB是平行四边形？
（2）在线段PB上是否存在一点Q，使得ODQP为菱形？若存在，求t的值；若不存在，请说明理由；
（3）△OPD为等腰三角形时，写出点P的坐标（不必写过程）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，在△ABC中，cos∠ABC=
，sin∠ACB= 
，AC=2，分别以AB，AC为边向△ABC形外作正方形ABGF和正方形ACDE，连接EF，点M是EF的中点，连接AM，则AM的长为 ． 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，BD是△ABC的角平分线，点E，F分别在BC，AB上，且DE∥AB，BE=AF．
（1）求证：四边形ADEF是平行四边形；
（2）若∠ABC=60°，BD=4，求平行四边形ADEF的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】为了贯彻落实国家关于增强青少年体质的计划，鄂州市全面实施了义务教育学段中小学学生“饮用奶计划”的营养工程．某牛奶供应商拟提供A（原味）、B（草莓味）、C（核桃味）、D（菠萝味）、E（香橙味）等五种口味的学生奶供学生选择（所有学生奶盒形状、大小相同），为了解对学生奶口味的喜好情况，某初级中学七年级（1）班李老师对全班同学进行了调查统计，制成了如图两幅不完整的统计图．
（1）该班五种口味的学生奶的喜好人数组成一组统计数据，直接写出这组数据的平均数，并将折线统计图补充完整．
（2）在进行调查统计的第二天，李老师为班上每位同学发放一盒学生奶．喜好A味的小聪和喜好B味的小明等四位同学最后领取，剩余的学生奶放在同一纸箱里，分别有A味2盒，B味和C味各1盒，李老师从该纸箱里随机取出两盒学生奶．请你用列表法或画树状图的方法，求出这两盒牛奶恰好同时是小聪和小明喜好的学生奶的概率．
相关试题
