【题目】如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形,建立如图所示的平面直角坐标系,点C的坐标为(0,﹣1).
(1)在如图的方格纸中把△ABC以点O为位似中心扩大,使放大前后的位似比为1:2,画出△A1B2C2(△ABC与△A1B2C2在位似中心O点的两侧,A,B,C的对应点分别是A1 , B2 , C2).
(2)利用方格纸标出△A1B2C2外接圆的圆心P,P点坐标是⊙P的半径= . (保留根号)
参考答案:
【答案】
(1)
解:如图,△A1B2C2为所作

(2)(3,1);![]()
【解析】解: (2)点P的坐标为(3,1),
PA1= ![]() =
= ![]() ,
,
即⊙P的半径为 ![]() .
.
故答案为(3,1), ![]() .
.
(1)利用关于原点为位似中心的两图形的对应的坐标关系写出点A1 , B2 , C2的坐标,然后描点即可得到△A1B2C2;(2)利用网格特点,作A1C2和C2B2的垂值平分线得到△A1B2C2外接圆的圆心P,然后写出P点坐标和计算PA1 .
-
科目: 来源: 题型:
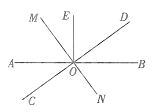
查看答案和解析>>【题目】如图,直线AB,CD,OE⊥AB,过点O画直线MN⊥CD. 若点F是直线MN上任意一点(点O除外),且∠AOC=34°.求∠EOF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是以原点为圆心,2
 为半径的圆,点P是直线上y=﹣x+8的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
为半径的圆,点P是直线上y=﹣x+8的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( ) 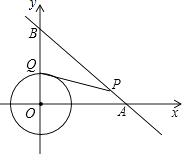
A.4
B.2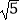
C.8﹣2
D.2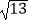
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:2tan60°﹣(
 )﹣1+(﹣2)2×(2017﹣sin45°)0﹣|﹣
)﹣1+(﹣2)2×(2017﹣sin45°)0﹣|﹣ 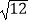 |
| -
科目: 来源: 题型:
查看答案和解析>>【题目】将一幅三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.

(1)求证:CF∥AB.
(2)求∠DFC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,射线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF。
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC∶∠OFC的值是否随之变化?若变化,找出变化规律;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.
(1)若∠BAC=50°,求∠EDA的度数;
(2)求证:直线AD是线段CE的垂直平分线.

相关试题

