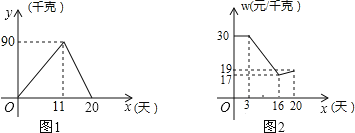
【题目】小明家今年种植的草莓喜获丰收,采摘上市20天全部销售完,爸爸让他对今年的销售情况进行跟踪记录,小明利用所学的数学知识将记录情况绘成图象(所得图象均为线段),日销售量y(单位:千克)与上市时间x(单位:天)的函数关系如图1所示,草莓的价格w(单位:元/千克)与上市时间x(单位:天)的函数关系如图2所示.
(1)观察图象,直接写出当0≤x≤11时,日销售量y与上市时间x之间的函数解析式为 ;
当11≤x≤20时,日销售量y与上市时间x之间的函数解析式为 .
(2)试求出第11天的销售金额;
(3)若上市第15天时,爸爸把当天能销售的草莓批发给了邻居马叔叔,批发价为每千克15元,马叔叔到市场按照当日的价格w元/千克将批发来的草莓全部销售完,他在销售的过程中,草莓总质量损耗了2%.那么,马叔叔支付完来回车费20元后,当天能赚到多少元?
参考答案:
【答案】(1)y=![]() x,y=-10x+200;(2)第11天的销售总额为1980元;(3)112元.
x,y=-10x+200;(2)第11天的销售总额为1980元;(3)112元.
【解析】试题分析:(1)当0≤x≤11时,设y与x之间的函数关系式为y=kx,当11≤x≤20时设y与x之间的函数关系式为y=k1x+b,由待定系数法求出其解即可;
(2)当3≤x<16时,设w与x的关系式为w=k2x+b2,当x=11时,代入解析式求出w的值,由销售金额=单价×数量就可以求出结论;
(3)当x=15时代入(1)的解析式求出y的值,再当x=15时代入(2)的解析式求出w的值,再由利润=销售总额-进价总额-车费就可以得出结论.
试题解析:
(1)当0≤x≤11时,设y与x之间的函数关系式为y=kx,
当11≤x≤20时设y与x之间的函数关系式为y=k1x+b,由题意,得
90=11k, ![]() ,
,
解得:k=![]() ,
,
![]() ,
,
∴y=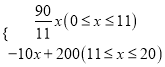 ,
,
故答案为:y= ![]()
y=-10x+200;
(2)当3≤x<16时,设w与x的关系式为w=k2x+b2,由题意,得
![]() ,
,
解得: ![]() ,
,
∴w=-x+33.
当x=11时,
y=90,w=22,
∴90×22=1980元.
答:第11天的销售总额为1980元;
(3)由题意,得
当x=15时,
y=-10×15+200=50千克.
w=-15+33=18元,
利润为:50(1-2%)×18-50×15-20=112元.
答:当天能赚到112元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学习小组利用三角形相似测量学校旗杆的高度.测得身高为1.6米小明同学在阳光下的影长为1米,此时测得旗杆的影长为9米.则学校旗杆的高度是( )
A.9米B.14.4米C.16米D.13.4米
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:正方形ABCD,等腰直角三角板的直角顶点落在正方形的顶点D处,使三角板绕点D旋转.
(1)当三角板旋转到图1的位置时,猜想CE与AF的数量关系,并加以证明;
(2)在(1)的条件下,若DE:AE:CE= 1:
 :3,求∠AED的度数;
:3,求∠AED的度数;(3)若BC= 4,点M是边AB的中点,连结DM,DM与AC交于点O,当三角板的一边DF与边DM重合时(如图2),若OF=
 ,求CN的长.
,求CN的长.
-
科目: 来源: 题型:
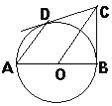
查看答案和解析>>【题目】AB为⊙O直径,BC为⊙O切线,切点为B,CO平行于弦AD,作直线DC.
(1)求证:DC为⊙O切线;
(2) 若AD·OC=8,求⊙O半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形既是中心对称图形又是轴对称图形的是( )
A.等腰三角形B.等边三角形C.圆D.平行四边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某周七天的最高气温统计如下表:
最高气温(℃)
25
26
27
28
天数
1
1
2
3
求这组数据的中位数与众数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a<0,则不等式﹣ax+a<0的解集是( )
A. x<1 B. x>1 C. x<﹣1 D. x>﹣1
相关试题

