【题目】我们知道,任意一个正整数n都可以进行这样的分解:![]() (p,q是正整数,且
(p,q是正整数,且![]() ),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的完美分解.并规定:
),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的完美分解.并规定:![]() .
.
例如18可以分解成1×18,2×9或3×6,因为18-1>9-2>6-3,所以3×6是18的完美分解,所以F(18)=![]() .
.
(1)F(13)= ,F(24)= ;
(2)如果一个两位正整数t,其个位数字是a,十位数字为![]() ,交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数为“和谐数”,求所有“和谐数”;
,交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数为“和谐数”,求所有“和谐数”;
(3)在(2)所得“和谐数”中,求F(t)的最大值.
参考答案:
【答案】(1)![]() ,
,![]() (2)所以和谐数为15,26,37,48,59;(3)F(t)的最大值是
(2)所以和谐数为15,26,37,48,59;(3)F(t)的最大值是![]() .
.
【解析】
(1)根据题意,按照新定义的法则计算即可.
(2)根据新定义的”和谐数”定义,将数用a,b表示列出式子解出即可.
(3)根据(2)中计算的结果求出最大即可.
解:(1)F(13)=![]() ,F(24)=
,F(24)=![]() ;
;
(2)原两位数可表示为![]()
新两位数可表示为![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]() (
(![]() 且b为正整数 )
且b为正整数 )
∴b=2,a=5; b=3,a=6, b=4,a=7,
b=5,a=8 b=6,a=9
所以和谐数为15,26,37,48,59
(3)所有“和谐数”中,F(t)的最大值是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)
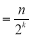 (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=13,则:
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=13,则: 若n=24,则第100次“F”运算的结果是________.
若n=24,则第100次“F”运算的结果是________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在□ABCD中,点G为对角线AC的中点,过点G的直线EF分别交边AB、CD于点E、F,过点G的直线MN分别交边AD、BC于点M、N,且∠AGE=∠CGN.

(1)求证:四边形ENFM为平行四边形;
(2)当四边形ENFM为矩形时,求证:BE=BN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线
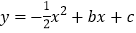 与x轴交于点A、B,与y轴交于点C,直线y=x+4经过点A、C,点P为抛物线上位于直线AC上方的一个动点.
与x轴交于点A、B,与y轴交于点C,直线y=x+4经过点A、C,点P为抛物线上位于直线AC上方的一个动点.(1)求抛物线的表达式;
(2)如图,当CP//AO时,求∠PAC的正切值;
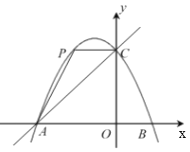
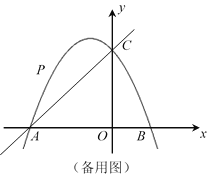
(3)当以AP、AO为邻边的平行四边形第四个顶点恰好也在抛物线上时,求出此时点P的坐标.
-
科目: 来源: 题型:
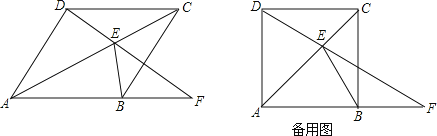
查看答案和解析>>【题目】如图,四边形ABCD为菱形,E为对角线AC上的一个动点,连结DE并延长交射线AB于点F,连结BE.
(1)求证:∠AFD=∠EBC;
(2)若∠DAB=90°,当△BEF为等腰三角形时,求∠EFB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条笔直的公路上依次有A,C,B三地,甲、乙两人同时出发,甲从A地骑自行车去B地,途经C地休息1分钟,继续按原速骑行至B地,甲到达B地后,立即按原路原速返回A地;乙步行从B地前往A地.甲、乙两人距A地的路程y(米)与时间x(分)之间的函数关系如图所示,请结合图象解答下列问题:
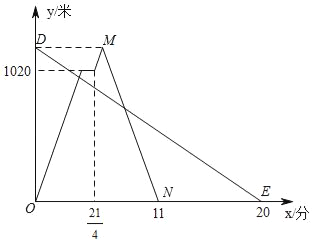
(1)请写出甲的骑行速度为 米/分,点M的坐标为 ;
(2)求甲返回时距A地的路程y与时间x之间的函数关系式(不需要写出自变量的取值范围);
(3)请直接写出两人出发后,在甲返回A地之前,经过多长时间两人距C地的路程相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E、F、H分别是AB、BC、CD的中点,CE、DF交于点G,连接AG、HG。下列结论:①CE⊥DF;②AG=DG;③∠CHG=∠DAG。其中,正确的结论有( )

A. 0个B. 1个C. 2个D. 3个
相关试题

