【题目】如图,△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,B,C,D在同一直线上,连接EC.求证:EC⊥BD. 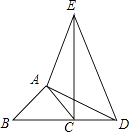
参考答案:
【答案】证明:∵在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,
∴∠BAC+∠CAD=∠EAD+∠CAD,∠ABC=∠BCA=45°,
∴∠BAD=∠CAE,
在△ABD和△ACE 中,
∴△ABD≌△ACE,
∴∠ACE=∠ABD=∠ABC=45°,
∴∠BCA+∠ACE=90°,
∴EC⊥BD
【解析】先根据∠BAC+∠CAD=∠EAD+∠CAD,得出∠BAD=∠CAE,然后证明△ABD≌△ACE,再得出∠ACE=∠ABD=45°,∠BCA+∠ACE=90°,即可证明出EC⊥BD.
【考点精析】本题主要考查了等腰直角三角形的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运动属于平移的是 ( )
A. 篮球运动员投出的篮球的运动 B. 空中放飞的风筝的运动
C. 乒乓球比赛中乒乓球的运动 D. 飞机在跑道上滑行到停止的运动
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2+3=2x的根的情况为( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.有一个实数根
D.没有实数根 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个盒子里装有标号为1,2,3,4,5,6,7,8,9,10的十个小球,这些小球除标号数字之外都相同,甲,乙二人用这些小球玩游戏,规则是:甲、乙先后从盒子里摸球(不放回),谁摸到的标号数字大,谁就获胜.
(1)第一轮游戏:若甲先摸到了1号球,求甲获胜的概率;
(2)第二轮游戏:若甲先摸到了10号球,求甲获胜的概率;
(3)第三轮游戏:若甲先摸到了3号球,那么甲、乙获胜的概率分别是多少. -
科目: 来源: 题型:
查看答案和解析>>【题目】要了解一批投影仪的使用寿命,从中任意抽取40台投影仪进行试验,在这个问题中,样本是( )
A. 每台投影仪的使用寿命 B. 一批投影仪的使用寿命
C. 40台投影仪的使用寿命 D. 40
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解方程x2﹣2x﹣5=0时,原方程应变形为( )
A.(x+1)2=6
B.(x+2)2=9
C.(x﹣1)2=6
D.(x﹣2)2=9 -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程组:
(1)
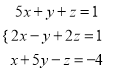
(2)
 .
.
相关试题

