【题目】(阅读材料)
我们知道“在数轴上表示的两个数,右边的数总比左边的数大”,利用此规律,我们可以求数轴上两个点之间的距离,具体方法是:用右边的数减去左边的数的差就是表示这两个数的两点之间的距离.若点![]() 表示的数是
表示的数是![]() ,点
,点![]() 表示的数是
表示的数是![]() ,点
,点![]() 在点
在点![]() 的右边(即
的右边(即![]() ),则点
),则点![]() ,
,![]() 之间的距离为
之间的距离为![]() (即
(即![]() ).
).
例如:若点![]() 表示的数是-6,点
表示的数是-6,点![]() 表示的数是-9,则线段
表示的数是-9,则线段![]() .
.
(理解应用)
(1)已知在数轴上,点![]() 表示的数是-2020,点
表示的数是-2020,点![]() 表示的数是2020,求线段
表示的数是2020,求线段![]() 的长;
的长;
(拓展应用)
如图,数轴上有三个点,点![]() 表示的数是-2,点
表示的数是-2,点![]() 表示的数是3,点
表示的数是3,点![]() 表示的数是
表示的数是![]() .
.
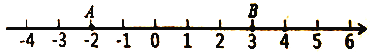
(2)当![]() ,
,![]() ,
,![]() 三个点中,其中一个点是另外两个点所连线段的中点时,求
三个点中,其中一个点是另外两个点所连线段的中点时,求![]() 的值;
的值;
(3)在点![]() 左侧是否存在一点
左侧是否存在一点![]() ,使点
,使点![]() 到点
到点![]() ,点
,点![]() 的距离和为19?若存在,求出点
的距离和为19?若存在,求出点![]() 表示的数:若不存在,请说明理由.
表示的数:若不存在,请说明理由.
参考答案:
【答案】(1)4040;(2)0.5,7或8;(3)-9.
【解析】
(1)根据题意,用点![]() 表示的数减去点
表示的数减去点![]() 表示的数加以计算即可;
表示的数加以计算即可;
(2)根据题意分①点![]() 是线段
是线段![]() 的中点、②点
的中点、②点![]() 是线段
是线段![]() 的中点、③点
的中点、③点![]() 是线段
是线段![]() 的中点三种情况进一步分析讨论即可;
的中点三种情况进一步分析讨论即可;
(3)设点![]() 表示的数是
表示的数是![]() ,然后分别表示出AQ与BQ,根据“点
,然后分别表示出AQ与BQ,根据“点![]() 到点
到点![]() ,点
,点![]() 的距离和为19”进一步求解即可.
的距离和为19”进一步求解即可.
(1)![]() ;
;
(2)①当点![]() 是线段
是线段![]() 的中点时,则
的中点时,则![]() .
.
所以![]() .解得:
.解得:![]() ;
;
②当点![]() 是线段
是线段![]() 的中点时,则
的中点时,则![]() .
.
所以![]() .解得:
.解得:![]() ;
;
③当点![]() 是线段
是线段![]() 的中点时,则
的中点时,则![]() .
.
所以![]() .解得:
.解得:![]() ;
;
综上所述,![]() 的值为0.5、
的值为0.5、![]() 或8;
或8;
(3)设点![]() 表示的数是
表示的数是![]() ,则:QA=
,则:QA=![]() ,QB=
,QB=![]() ,
,
∵![]() ,
,
∴![]() .
.
解得:![]() .
.
∴在点![]() 左侧存在一点
左侧存在一点![]() ,使点
,使点![]() 到点
到点![]() ,
,![]() 的距离和为19.且点
的距离和为19.且点![]() 表示的数是-9.
表示的数是-9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次数学课上,王老师出示一道题:解方程
 .小马立即举手并在黑板上写出了解方程过程,具体如下:
.小马立即举手并在黑板上写出了解方程过程,具体如下:解:
 ,
,去括号,得:
 .………………①
.………………①移项,得:
 .…………………②
.…………………②合并同类项,得:
 .……………………③
.……………………③系数化为1,得:
 .………………………④
.………………………④(1)请你写出小马解方程过程中哪步错了,并简要说明错误原因;
(2)请你正确解方程:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】美丽的洪泽湖周边景点密布.如图A,B为湖滨的两个景点,C为湖心一个景点.景点B在景点C的正东,从景点A看,景点B在北偏东75°方向,景点C在北偏东30°方向.一游客自景点
 驾船以每分钟20米的速度行驶了10分钟到达景点C,之后又以同样的速度驶向景点B,该游客从景点C到景点B需用多长时间(精确到1分钟)?
驾船以每分钟20米的速度行驶了10分钟到达景点C,之后又以同样的速度驶向景点B,该游客从景点C到景点B需用多长时间(精确到1分钟)?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠BAC=45°,若BD=2,CD=3,AD⊥BC于D,将△ABD沿AB所在的直线折叠,使点D落在点E处;将△ACD沿AC所在的直线折叠,使点D落在点F处,分别延长EB、FC使其交于点M.
(1)判断四边形AEMF的形状,并给予证明.
(2)设AD=x,利用勾股定理,建立关于x的方程模型,求四边形AEMF的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知整数a1,a2,a3,…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,…依此类推,则a2020的值为( )
A.
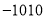 B.
B.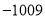 C.
C.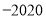 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线
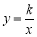 与直线
与直线 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线 于点E,交BD于点C.
于点E,交BD于点C.(1)若点D坐标是(-8,0),求A、B两点坐标及k的值.
(2)若B是CD的中点,四边形OBCE的面积为4,求直线CM的解析式.
(3)设直线AM、BM分别与y轴相交于P、Q两点,且MA=pMP,MB=qMQ,求p-q的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解不等式:
 ,并把它的解集表示在数轴上;
,并把它的解集表示在数轴上;(2)解不等式组
 ,并写出它的所有非负整数解.
,并写出它的所有非负整数解.
相关试题

